O Howland Current Pump é um circuito amplamente utilizado para converter tensão em uma corrente constante, independentemente das variações na resistência da carga. Este circuito é fundamental em sistemas de controle, instrumentação médica e outras aplicações que exigem precisão. Neste artigo, vamos explorar em detalhes o funcionamento do circuito, as fórmulas envolvidas no cálculo de seus componentes e apresentar um exemplo prático acompanhado de simulação em software.
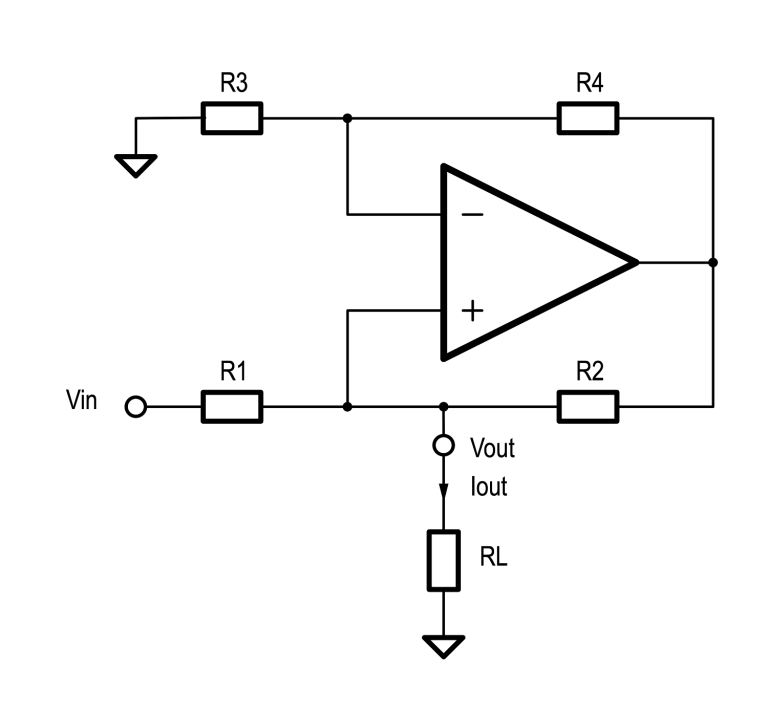
Fundamentos do Howland Current Pump
O circuito Howland Current Pump utiliza um amplificador operacional (op-amp) configurado de forma a garantir que a corrente de saída seja constante, independentemente das mudanças na resistência da carga. Isso é possível graças a uma rede de resistores conectados ao op-amp, que regula a corrente de saída com base na tensão de entrada.
Equações Fundamentais
A análise do circuito começa com a aplicação da Lei de Kirchhoff das Correntes (KCL) e da Lei de Ohm. A corrente de saída \( I_{out} \) é a soma das correntes através dos resistores \( R_3 \) e \( R_4 \), que podem ser expressas da seguinte forma:
\[
I_{out} = \left(\frac{V_1 – V_L}{R_3}\right) + \left(\frac{V_A – V_L}{R_4}\right)
\]
Onde:
- \( V_1 \) é a tensão de entrada,
- \( V_L \) é a tensão sobre a carga,
- \( V_A \) é a tensão de saída do op-amp.
O op-amp está configurado como um amplificador não-inversor com ganho \( A \), determinado pelos resistores \( R_1 \) e \( R_2 \):
\[
V_A = \left(1 + \frac{R_2}{R_1}\right) \cdot V_L
\]
Substituindo essa equação na fórmula de ( I_{out} ), obtemos:
\[
I_{out} = \left(\frac{V_1 – V_L}{R_3}\right) + \left[\left(1 + \frac{R_2}{R_1}\right) \cdot V_L – \frac{V_L}{R_4}\right]
\]
Para que a corrente de saída seja independente da tensão de carga ( V_L ), a condição de balanceamento dos resistores deve ser atendida:
\[
\frac{R_4}{R_3} = \frac{R_2}{R_1}
\]
Essa equação é fundamental para garantir que a corrente de saída seja controlada pela tensão de entrada e pelos resistores, e não pela resistência da carga.
Análise Detalhada do Circuito
Passo a Passo para o Cálculo dos Componentes
1. Definição da Corrente de Saída \(( I_{out} )\)
O primeiro passo é definir a corrente que o circuito precisa fornecer à carga. A corrente de saída é o parâmetro mais importante e deve ser escolhido com base na aplicação desejada.
2. Escolha do Resistor \( R_3 \)
O resistor \( R_3 \) é diretamente relacionado à corrente de saída, conforme a equação:
\[
I_{out} = \frac{V_{in}}{R_3}
\]
Escolha ( R_3 ) com base na corrente de saída desejada e na tensão de entrada disponível. Por exemplo, se você deseja uma corrente de 10 mA e uma tensão de entrada de 10 V, ( R_3 ) será:
\[
R_3 = \frac{V_{in}}{I_{out}} = \frac{10V}{10mA} = 1k\Omega
\]
3. Definição dos Resistores \( R_1 \) e \( R_2 \)
Os resistores \( R_1 \) e \( R_2 \) definem o ganho do op-amp. Em muitas aplicações, \( R_1 \) e \( R_2 \) são escolhidos para que \( A = 2 \), o que é adequado para muitas situações práticas. Um par típico é \( R_1 = R_2 = 10k\Omega \).
4. Cálculo de ( R_4 )
Com base na condição de balanceamento, o resistor ( R_4 ) é calculado pela fórmula:
\[
R_4 = \frac{R_2 \cdot R_3}{R_1}
\]
Se ( R_1 = R_2 = 10k\Omega ) e ( R_3 = 1k\Omega ), então:
\[
R_4 = \frac{10k\Omega \cdot 1k\Omega}{10k\Omega} = 1k\Omega
\]
5. Verificação da Condição de Balanceamento
Certifique-se de que a condição \( \frac{R_4}{R_3} = \frac{R_2}{R_1} \) é satisfeita. Isso garante que o circuito funcione corretamente, mantendo a corrente de saída constante, independentemente da resistência da carga.
Exemplo Prático Detalhado
Vamos aplicar o passo a passo para projetar um circuito que forneça uma corrente de saída constante de 5 mA, utilizando uma tensão de entrada de 10 V.
1. Definição de ( I_{out} ) e ( V_{in} )
- \( I_{out} = 5mA \)
- \( V_{in} = 10V \)
2. Escolha de \( R_3 \)
Usando a equação \( I_{out} = \frac{V_{in}}{R_3} \):
\[
R_3 = \frac{V_{in}}{I_{out}} = \frac{10V}{5mA} = 2k\Omega
\]
3. Definição de \( R_1 \) e \( R_2 \)
Escolhemos \( R_1 = R_2 = 10k\Omega \), o que define o ganho do op-amp como:
\[
A = 1 + \frac{R_2}{R_1} = 2
\]
4. Cálculo de \( R_4 \)
Agora, usando a equação de balanceamento:
\[
R_4 = \frac{R_2 \cdot R_3}{R_1} = \frac{10k\Omega \cdot 2k\Omega}{10k\Omega} = 2k\Omega
\]
5. Verificação da Condição de Balanceamento
Verificamos que:
\[
\frac{R_4}{R_3} = \frac{2k\Omega}{2k\Omega} = 1 \quad \text{e} \quad \frac{R_2}{R_1} = \frac{10k\Omega}{10k\Omega} = 1
\]
A condição de balanceamento é satisfeita, confirmando que o circuito fornecerá uma corrente constante de 5 mA.
6. Simulação com LTspice ou Qspice
Após o cálculo teórico, você pode utilizar os softwares LTspice ou Qspice para simular o circuito e verificar seu comportamento.
- Configuração da Simulação: Insira os valores calculados no software, configure o op-amp e os resistores.
- Análise dos Resultados: A simulação mostrará que, mesmo variando a resistência de carga, a corrente de saída permanece constante em 5 mA.
Essa simulação é fundamental para validar o projeto antes de sua implementação física, garantindo que o circuito funcione corretamente.
Conclusão
O Howland Current Pump é um circuito versátil e eficiente para aplicações que exigem conversão de tensão em corrente constante. Com uma compreensão detalhada das equações e parâmetros de projeto, é possível configurar o circuito para atender a diversas necessidades. As variações, como o Improved Howland Current Pump, expandem ainda mais sua utilidade, permitindo maior precisão e estabilidade em situações que envolvem altas correntes ou cargas reativas. Ao utilizar ferramentas de simulação como LTspice e Qspice, você pode garantir a eficácia do design teórico na prática.
Referências
- Howland Current Pump Circuit Simulation Project – Naman Girdhar, orientado por Dr. Maheshwari.R, SCOPE VIT Chennai. Disponível no documento: Howland_Current_Pump_Circuit.pdf.
- The Howland Current Pump – Artigo detalhado sobre o circuito, incluindo a operação básica e a análise matemática. Disponível no documento: ourdev_694588RI0RBJ.pdf.
- Analysis of Improved Howland Current Pump Configurations (Rev. A) – Ignacio Vazquez Lam, Texas Instruments. Documento completo sobre as variações do circuito Howland Current Pump. Disponível no documento: sboa437a.pdf.
- Howland Current Source – Circuit Cellar. Artigo online explicando o funcionamento do circuito Howland Current Source, incluindo uma tabela comparativa de tensões e imagem introdutória do circuito. Disponível em: Circuit Cellar.
- The Howland Current Pump – All About Circuits. Artigo técnico explicando o funcionamento detalhado do circuito Howland Current Pump. Disponível em: All About Circuits.
Sobre o Autor
