Em matemática, o limite é uma ferramenta fundamental do cálculo diferencial e integral. Ele permite descrever o comportamento de uma função à medida que a variável independente se aproxima de um determinado valor. O limite responde perguntas como: “Qual o valor que uma função se aproxima quando x se aproxima de um ponto específico?”
Por exemplo, ao estudar circuitos eletrônicos com sinais que mudam rapidamente — como em um degrau de tensão — podemos querer saber qual é o comportamento da corrente quando o tempo tende a zero. O conceito de limite é o que torna possível essa análise rigorosa, mesmo quando o valor exato da função naquele ponto não está bem definido.
Por que estudar Limites na Eletrônica?
Na eletrônica, os limites aparecem em diversas situações, tais como:
- Análise de respostas transitórias: Quando ligamos um capacitor ou um indutor, a corrente ou a tensão não mudam instantaneamente. O limite ajuda a entender o que acontece nos instantes iniciais.
- Circuitos com funções descontínuas ou com sinais degrau: Para analisar a continuidade ou descontinuidade.
- Derivadas e integrais: Derivadas (taxas de variação) e integrais (áreas sob curvas), usadas em filtros, controles e sinais, dependem da definição de limite.
- Modelagem de semicondutores: O comportamento da corrente em função da tensão em diodos ou transistores envolve funções exponenciais e seus limites em extremos.
A seguir, apresentarei seis exemplos distintos de limites, classificados como:
- Dois limites existentes e definidos
- Dois limites que não existem
- Dois limites infinitos
Cada exemplo será acompanhado de explicação e gráfico, ideal para quem está começando a estudar cálculo com foco em aplicações práticas.
O segundo exemplo possui uma indeterminação no ponto x = 1, o que é comum em problemas de limite. Vamos corrigi-lo para evitar essa divisão por zero durante o gráfico e mostrar apenas o comportamento ao redor do ponto (sem tentar calcular o valor diretamente em x = 1).
Vamos seguir com a correção e exibir os dois gráficos corretamente.
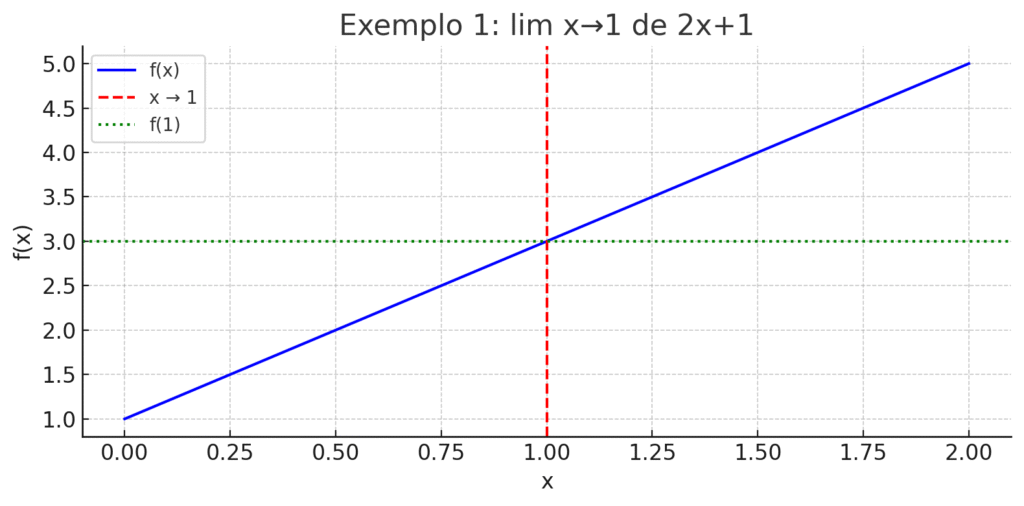
Exemplo 1: Limite de uma função contínua
Função: \[f(x) = 2x + 1\]
Limite quando \[x→1x \to 1x→1\]:\[\lim_{x \to 1} (2x + 1) = 3x→1\]
Essa função é contínua e definida para todos os valores de xxx, ou seja, o valor da função no ponto é igual ao limite quando nos aproximamos desse ponto.
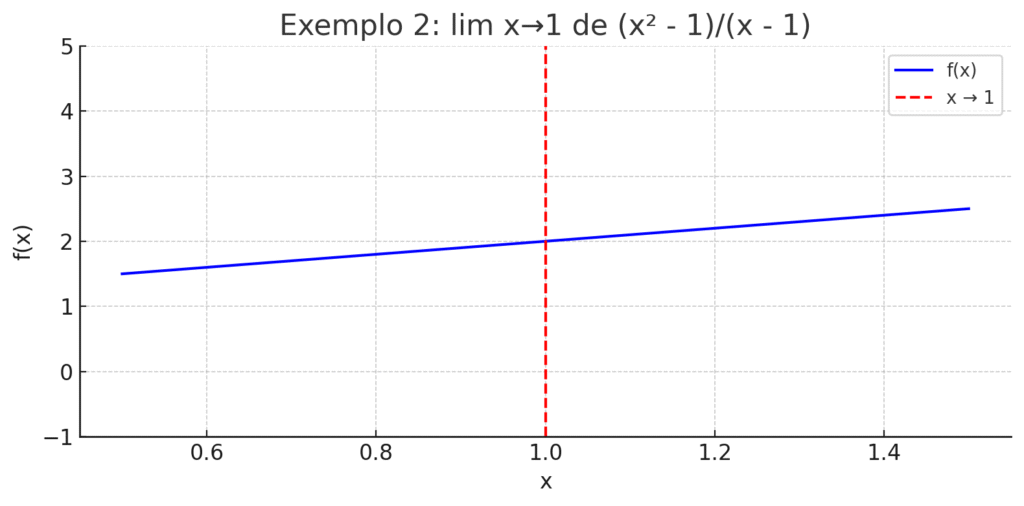
Exemplo 2: Limite com indeterminação removível
Função: \[f(x) = \frac{x^2 – 1}{x – 1}\]
Note que: \[x^2 – 1 = (x – 1)(x + 1) \Rightarrow f(x) = \frac{(x – 1)(x + 1)}{x – 1} = x + 1 \quad \text{(para } x \neq 1\text{)}\]
Limite quando \(x→1x \to 1x→1\): \[\lim_{x \to 1} \frac{x^2 – 1}{x – 1} = \lim_{x \to 1} (x + 1) = 2x→1\]
Esse é um exemplo clássico de discontinuidade removível, muito útil para entender como limites permitem estudar funções que “quase” têm valor em um ponto.
Exemplo 3: Lim X→0 De Sin(1/X)
Exemplo 4: Lim X→0 De Função Por Partes
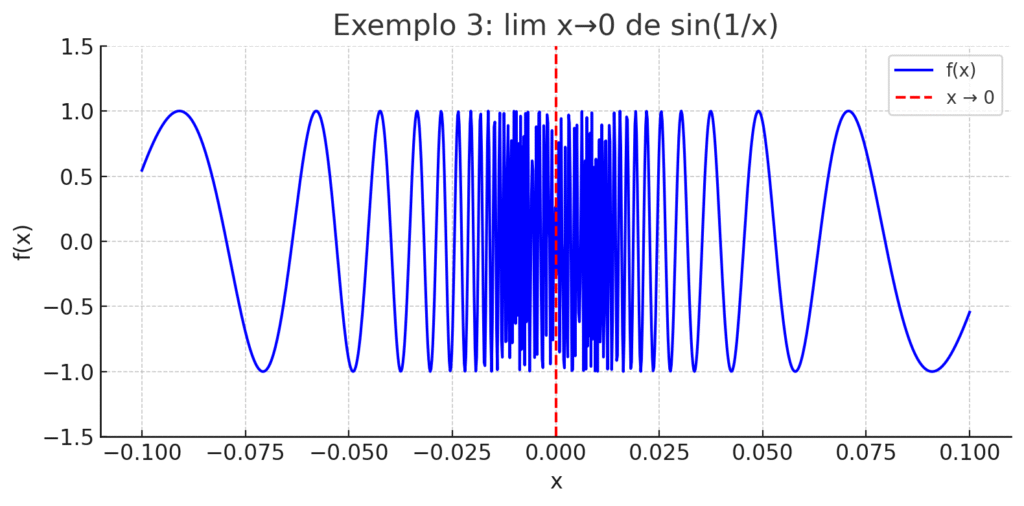
Exemplo 3: Limite que não existe por oscilação
Função: \[f(x) = \sin\left(\frac{1}{x}\right)\]
Limite quando \[x→0x \to 0x→0\]:
Este limite não existe porque, à medida que xxx se aproxima de zero, o argumento do seno tende ao infinito, fazendo com que a função oscile infinitamente entre -1 e 1. Isso é típico em sistemas com instabilidade de alta frequência ou em fenômenos com ruídos não determinísticos em torno de zero, comuns na eletrônica de RF (radiofrequência).
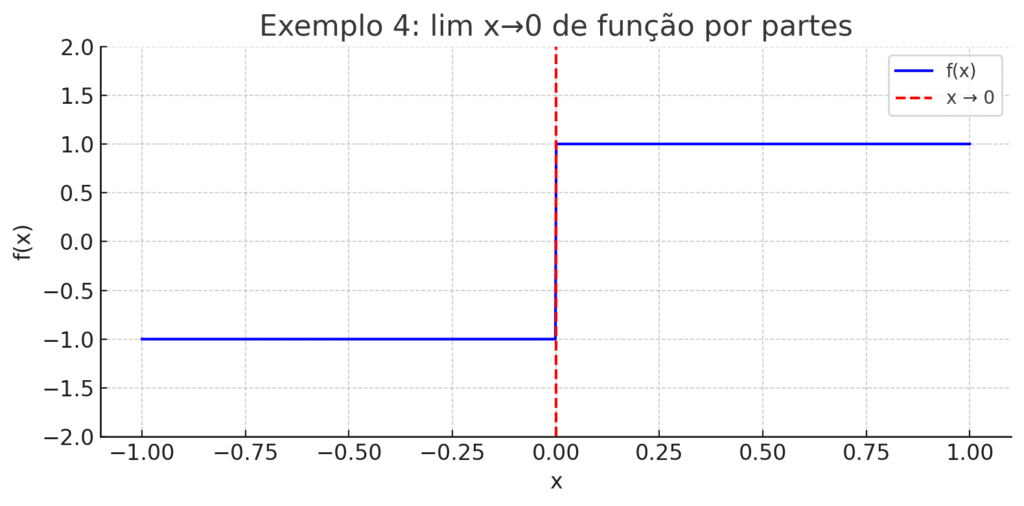
Exemplo 4: Limite com laterais diferentes
Função por partes: \[f(x) = \begin{cases} -1 & \text{se } x < 0 \\ 1 & \text{se } x \geq 0 \end{cases}\]
Limite quando \(x→0x \to 0x→0:\)
Esse limite não existe, pois o limite pela esquerda é -1 e pela direita é 1. Essa situação ocorre, por exemplo, em sinais de chaveamento digital ou comutação instantânea em um circuito, como no acionamento de relés ou transistores em uma borda de clock. O limite ajuda a prever comportamentos divergentes nesses pontos críticos.
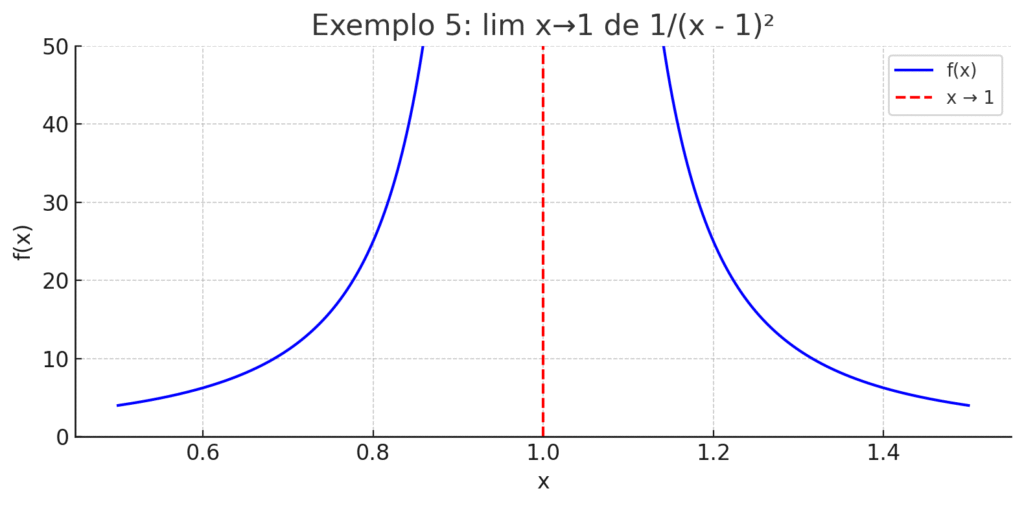
Exemplo 5: \(Lim X→1 De 1/(X – 1)^2\)
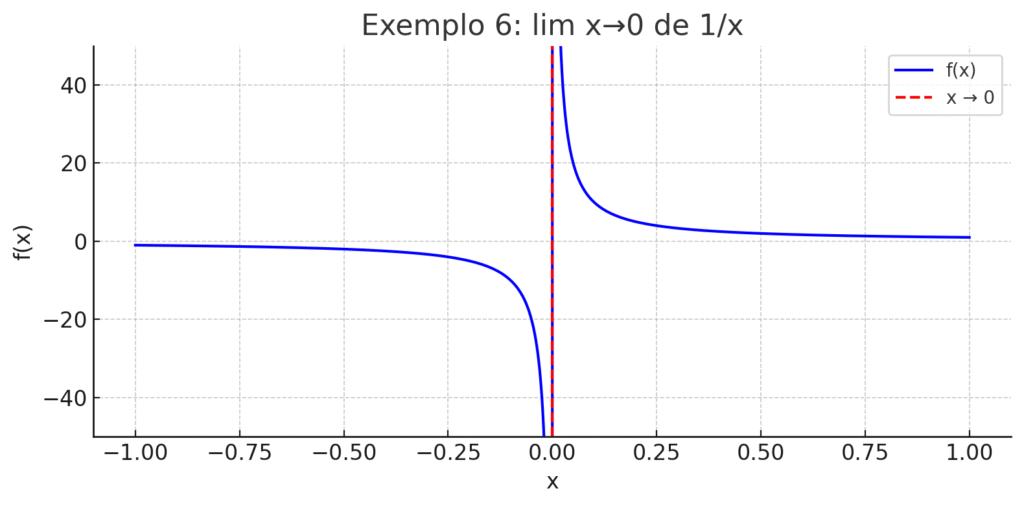
Exemplo 6: Lim X→0 De 1/X
Aqui estão os dois exemplos de limites infinitos, fundamentais para compreender assíntotas verticais e comportamentos extremos em sistemas eletrônicos:
Exemplo 5: Limite infinito positivo
Função: \[f(x) = \frac{1}{(x – 1)^2}\]
Limite quando \(x→1x \to 1x→1\): \[\lim_{x \to 1} \frac{1}{(x – 1)^2} = \infty\]
Conforme xxx se aproxima de 1 (por qualquer lado), o denominador se aproxima de zero, e o valor da função cresce indefinidamente. Esse comportamento é comum em modelos de resposta de circuitos com picos de ressonância, onde uma frequência específica gera uma energia que cresce rapidamente, como em filtros LC ressonantes.
Exemplo 6: Limite com assíntota vertical e sinal alternado
Função: \[f(x) = \frac{1}{x}\]
Limite quando x→0x \to 0x→0:
- Pelo lado positivo: \[\lim_{x \to 0^+} \frac{1}{x} = \infty\]
- Pelo lado negativo: \[\lim_{x \to 0^-} \frac{1}{x} = -\infty\]
Esse tipo de função possui uma assíntota vertical no zero, e o comportamento diverge para sinais opostos conforme nos aproximamos do ponto. É um modelo clássico usado em circuitos com inversores, multiplicadores analógicos ou até na modelagem da impedância de capacitores e indutores em baixíssimas frequências, onde o valor tende ao infinito ou ao zero de forma assimétrica.
Sobre o Autor
