O cálculo da impedância de saída em amplificadores é fundamental para entender como o circuito reage à carga conectada, influenciando diretamente no desempenho. No caso de um amplificador Classe A polarizado por divisor de tensão na base, o conhecimento detalhado dos componentes do circuito e suas contribuições para a impedância de saída é crucial. Este artigo vai ensinar, passo a passo, como calcular a impedância de saída de um amplificador desse tipo usando um transistor bipolar.
Conceitos Iniciais: Polarização por Divisor de Tensão
A polarização de base por divisor de tensão é um método comum para garantir que o transistor funcione corretamente no regime ativo. O circuito típico envolve dois resistores conectados à base do transistor (R1 e R2), formando um divisor de tensão que estabelece a polarização da base. Além disso, temos o resistor de emissor (RE) e o resistor de coletor (RC), que também desempenham papéis importantes no funcionamento e nas características de impedância do circuito.
Nosso foco será calcular a impedância de saída, que depende de como esses componentes interagem em conjunto com o transistor.
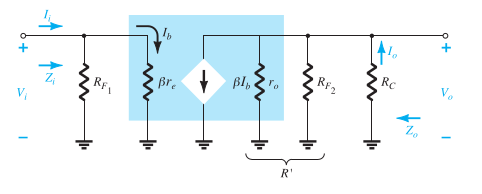
Cálculo da Impedância de Saída: Modelo de Pequeno Sinal
Para calcular a impedância de saída, usaremos o modelo de pequeno sinal do transistor. Nesse modelo, as correntes e tensões de polarização são substituídas por pequenas variações, que facilitam a análise do circuito em termos de impedâncias. A impedância de saída é influenciada por:
- A resistência de coletor (RC)
- A resistência do emissor (RE), vista através do fator de amplificação (β)
- A resistência interna do transistor (rπ), que é função da corrente de base e do parâmetro β.
A impedância de saída pode ser aproximada pela seguinte equação:
\[
Z_{out} \approx R_C \parallel \left( \frac{r_{\pi}}{\beta} + R_E \right)
\]
Onde:
- \(R_C\) é o resistor de coletor.
- \(R_E\) é o resistor de emissor.
- \(r_{\pi}\) é a resistência interna vista pela base do transistor, que depende da corrente de polarização.
Exemplo Prático: Cálculo da Impedância de Saída
Agora vamos aplicar os conceitos a um exemplo prático. Considere o seguinte circuito de um amplificador Classe A com um transistor bipolar (BJT):
- \(R_C = 1k\Omega\)
- \(R_E = 100\Omega\)
- \(r_{\pi} = 2.5k\Omega\)
- \(\beta = 100\)
Passo 1: Calcular a resistência vista pelo emissor
A resistência efetiva do emissor vista pela base é multiplicada pelo fator de amplificação \( \beta \), portanto:
\[
R_{E_{\text{eff}}} = \beta \times R_E = 100 \times 100\Omega = 10k\Omega
\]
Passo 2: Calcular a impedância de saída
Agora, aplicamos a fórmula da impedância de saída:
\[
Z_{out} \approx R_C \parallel \left( \frac{r_{\pi}}{\beta} + R_E \right)
\]
Substituindo os valores:
\[
Z_{out} \approx 1k\Omega \parallel \left( \frac{2.5k\Omega}{100} + 100\Omega \right)
\]
\[
Z_{out} \approx 1k\Omega \parallel (25\Omega + 100\Omega)
\]
\[
Z_{out} \approx 1k\Omega \parallel 125\Omega
\]
A impedância equivalente será:
\[
Z_{out} \approx \frac{1k\Omega \times 125\Omega}{1k\Omega + 125\Omega} \approx 111.1\Omega
\]
Portanto, a impedância de saída aproximada do amplificador é 111.1 Ω.
Conclusão
Compreender a impedância de saída de um amplificador Classe A permite otimizar o design e prever como ele interage com diferentes cargas. Neste exemplo, usamos os conceitos de modelo de pequeno sinal e componentes do circuito para calcular a impedância de saída, o que facilita o ajuste e a escolha de componentes no projeto de amplificadores.
Esse processo pode ser aplicado a outros tipos de amplificadores e configurações, desde que os parâmetros e o modelo equivalente sejam corretamente ajustados.
Sobre o Autor
