Os divisores de tensão são amplamente conhecidos por quem trabalha com eletrônica, especialmente no uso de resistores. No entanto, quando se trata de circuitos de corrente alternada (AC), os capacitores podem ser usados de maneira similar para dividir tensões de maneira eficiente.
Os divisores de tensão capacitivos são especialmente úteis em circuitos de alta frequência ou em aplicações onde é necessário reduzir tensões AC, como em sensores e sistemas de medição. Para entender o uso desses capacitores, é essencial saber como calculá-los e aplicar suas fórmulas corretamente.
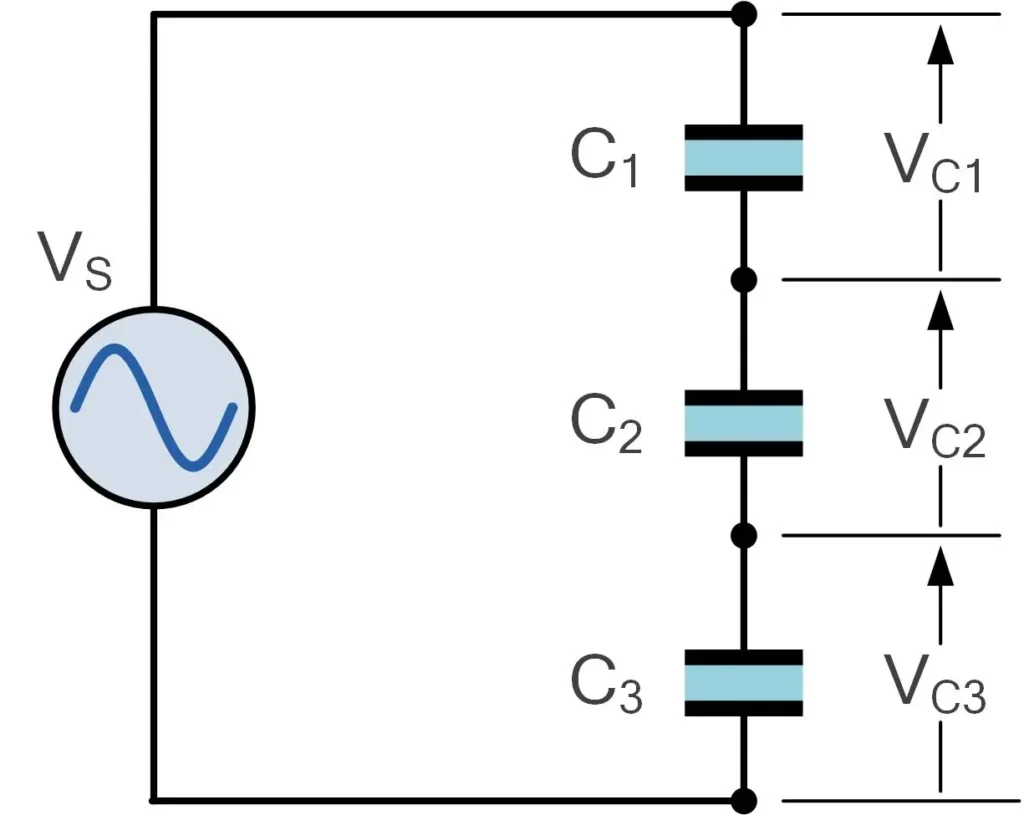
Funcionamento básico de um divisor capacitivo
Divisores capacitivos operam de maneira semelhante aos divisores resistivos, com a diferença de que, em vez de resistores, usamos capacitores para dividir a tensão em um circuito AC. Isso só é possível porque os capacitores, em circuitos de AC, têm uma propriedade chamada reatância capacitiva, que depende da frequência do sinal e da capacitância.
A reatância capacitiva é a oposição que um capacitor oferece à passagem de corrente alternada, e ela é inversamente proporcional à frequência do sinal e à capacitância do capacitor. Ou seja, quanto maior a frequência ou a capacitância, menor será a reatância.
A fórmula para calcular a reatância capacitiva é:
\[
X_C = \frac{1}{2\pi f C}
\]
Onde:
- \(X_C\) é a reatância capacitiva em ohms \(Ω\),
- \(f\) é a frequência do sinal em hertz \(Hz\),
- \(C\) é a capacitância em farads \(F\).
Nos divisores capacitivos, a tensão é dividida proporcionalmente entre os capacitores, de acordo com suas reatâncias, da mesma forma que a tensão é dividida entre resistores conforme suas resistências em um divisor resistivo.
Fórmulas para cálculo de divisores capacitivos
Agora que entendemos como funciona a reatância capacitiva, podemos aplicar as fórmulas de divisores de tensão para capacitores em série. Em um divisor de tensão capacitivo simples, dois capacitores são conectados em série, e a tensão de entrada é dividida entre eles.
A fórmula para a tensão (V_1) sobre o capacitor (C_1) em um divisor de dois capacitores (C_1) e (C_2) é dada por:
\[
V_1 = V_{in} \times \frac{X_{C1}}{X_{C1} + X_{C2}}
\]
Onde:
- \(V_1\) é a tensão sobre o capacitor \(C_1\),
- \(V_{in}\) é a tensão de entrada do circuito,
- \(X_{C1}\) e \(X_{C2}\) são as reatâncias capacitivas de \(C_1\) e \(C_2\), respectivamente.
Exemplo prático de cálculo
Vamos aplicar um exemplo prático para facilitar o entendimento. Suponha que temos uma tensão de entrada de 10V AC a uma frequência de 50Hz e dois capacitores de valores \(C_1 = 10\mu F\) e \(C_2 = 20\mu F\).
- Calcular a reatância de cada capacitor:
- Para \(C_1\):
\[
X_{C1} = \frac{1}{2\pi \times 50 \times 10 \times 10^{-6}} \approx 318 \, \Omega
\] - Para \(C_2\):
\[
X_{C2} = \frac{1}{2\pi \times 50 \times 20 \times 10^{-6}} \approx 159 \, \Omega
\]
- Calcular a tensão sobre \(C_1\):
- Usando a fórmula de divisor de tensão:
\[
V_1 = 10 \times \frac{318}{318 + 159} \approx 6.67 \, V
\]
Nesse caso, (C_1) teria uma tensão de 6.67V e (C_2) ficaria com o restante, 3.33V. Esse exemplo simples mostra como os capacitores dividem a tensão em função de suas reatâncias.
Aplicação prática
Os divisores capacitivos podem ser aplicados em diversas situações, como na redução de tensões AC em circuitos de medição ou em sensores que operam com sinais de alta frequência. Um exemplo prático seria o uso de divisores capacitivos para reduzir a tensão de entrada em circuitos de sensores de corrente alternada, onde precisamos monitorar a tensão sem usar transformadores volumosos.
No entanto, é importante lembrar que os divisores capacitivos não são adequados para aplicações onde se deseja lidar com altas correntes, pois os capacitores não dissipam potência como os resistores. Além disso, a tensão nos capacitores depende diretamente da frequência, o que pode limitar o uso em circuitos onde a frequência varia.
Considerações finais
O uso de capacitores como divisores de tensão em circuitos de AC é uma técnica útil e eficiente para determinadas aplicações, especialmente em situações de alta frequência. Compreender como calcular a reatância capacitiva e aplicar as fórmulas corretas para divisores de tensão é essencial para qualquer maker, técnico ou engenheiro que deseja projetar ou analisar circuitos de corrente alternada.
Se você gostou desse conteúdo e quer aprender mais sobre capacitores e suas aplicações, explore nossos outros tutoriais e continue aprofundando seus conhecimentos em eletrônica.
Sobre o Autor
