Por que Números Complexos Importam?
Quando falamos em números, a maioria de nós pensa em valores reais: 2, 3.14, -5, 0.001. No entanto, há um conjunto de números que transcende o eixo real e invade o plano bidimensional da matemática: os números complexos. Apesar de parecerem abstratos à primeira vista, eles estão intimamente ligados a aplicações concretas na engenharia elétrica, eletrônica, controle de sistemas e até mesmo em linguagens de programação que envolvem cálculos científicos ou simulações.
Um número complexo é uma extensão do conceito de número real. Ele possui duas partes: uma parte real e uma parte imaginária, esta última associada ao operador j (ou i, na matemática pura), que representa uma rotação de 90° no plano complexo.
Onde isso aparece na prática?
Na engenharia elétrica, por exemplo, os circuitos em corrente alternada (AC) envolvem componentes como resistores, capacitores e indutores. Esses elementos não apenas limitam a corrente, mas também introduzem defasagens de fase — isto é, mudanças no tempo entre tensão e corrente. Essa defasagem é elegantemente representada usando números complexos.
Imagine que você está desenvolvendo um programa para simular um circuito RLC (Resistor-Indutor-Capacitor) em Python, ou controlando um motor AC com um microcontrolador. Os números complexos não são apenas úteis — eles são essenciais. Eles nos permitem expressar tanto a magnitude quanto a fase das tensões e correntes, algo que os números reais não conseguem fazer sozinhos.
Representação Retangular e Operador j: A Essência dos Números Complexos
Um número complexo é representado da seguinte forma: z=a+jbz = a + jb
onde:
- a é a parte real do número;
- b é a parte imaginária;
- j é a unidade imaginária, definida como:
\[j = \sqrt{-1}\]
Na engenharia elétrica (ao contrário da matemática pura, que usa i), convencionou-se usar j para não confundir com a notação de corrente elétrica (i).
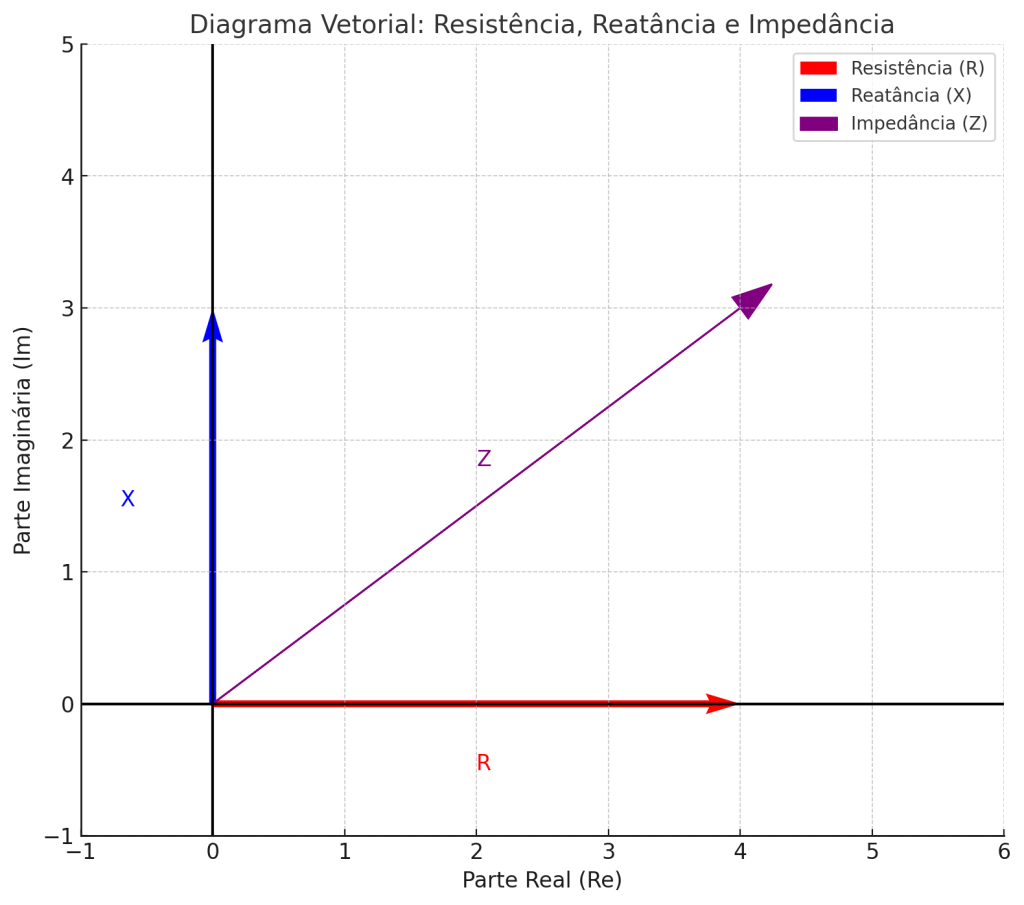
Essa forma é chamada de forma retangular ou forma binômial, pois expressa o número como uma soma (ou subtração) de duas componentes ortogonais: uma ao longo do eixo real (horizontal) e outra ao longo do eixo imaginário (vertical).
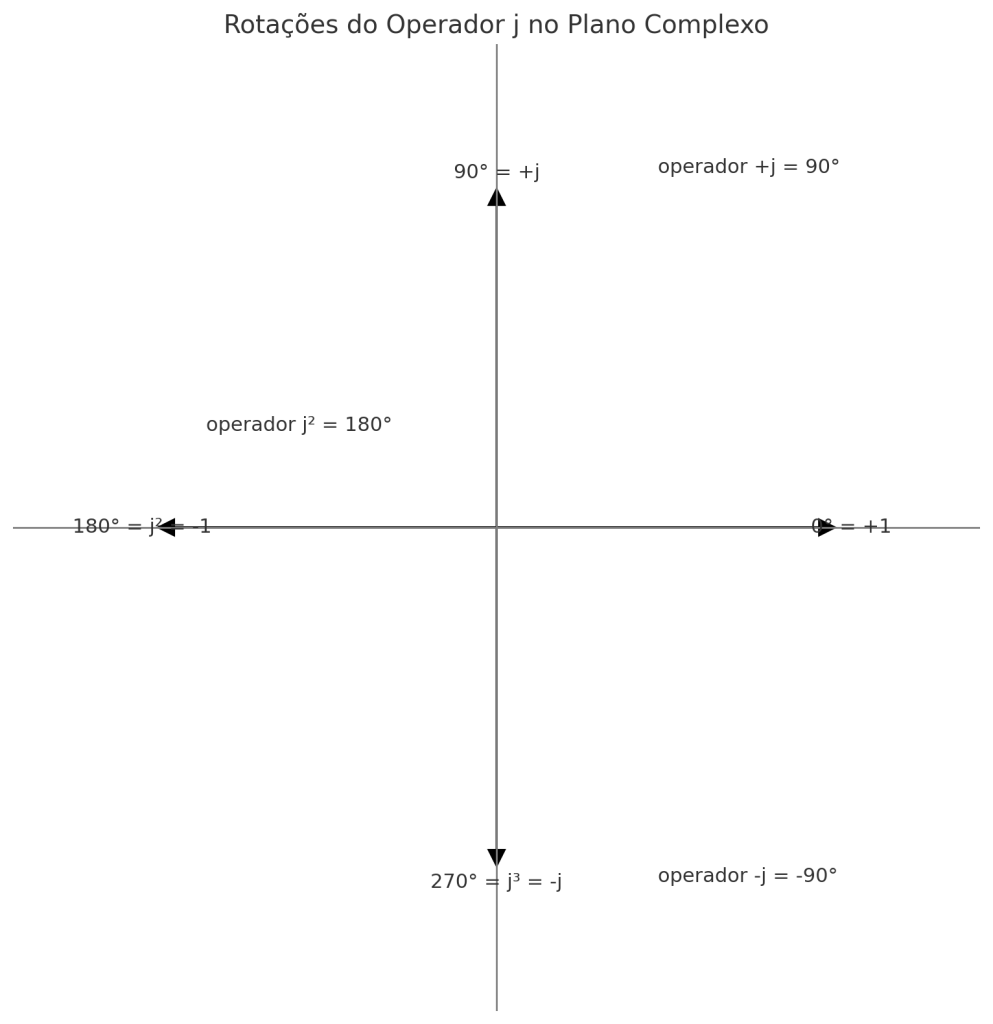
Entendendo o Operador j
O operador j representa uma rotação de 90° no plano complexo. Repetições sucessivas desse operador resultam em rotações múltiplas de 90°, obedecendo a seguinte sequência cíclica: \[\begin{aligned} j^0 &= 1 &&\text{(0°)} \\ j^1 &= j &&\text{(90°)} \\ j^2 &= -1 &&\text{(180°)} \\ j^3 &= -j &&\text{(270°)} \\ j^4 &= 1 &&\text{(360°, volta à origem)} \\ \end{aligned}\]
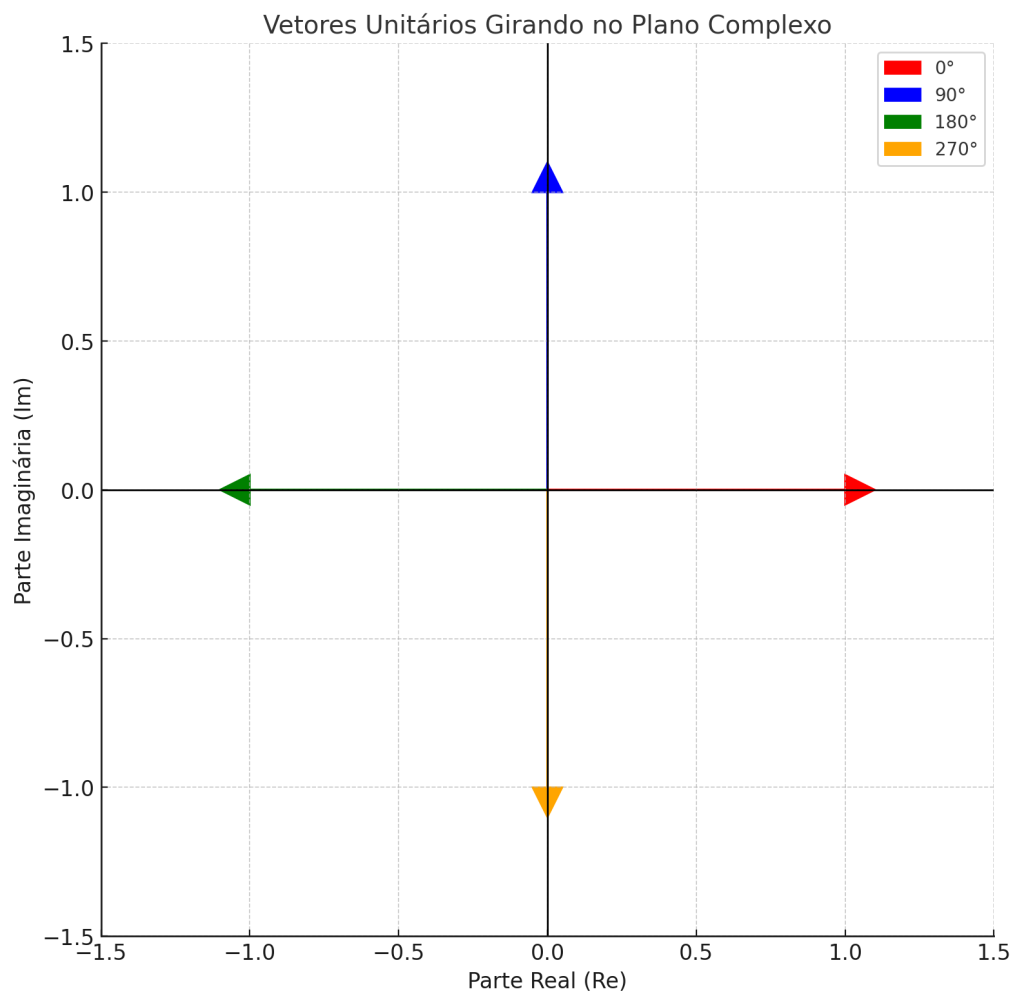
Essa ciclicidade é fundamental na análise de circuitos AC, onde defasagens de ±90° são comuns ao lidar com capacitores e indutores.
Exemplo Prático: Reatância Representada por Números Complexos
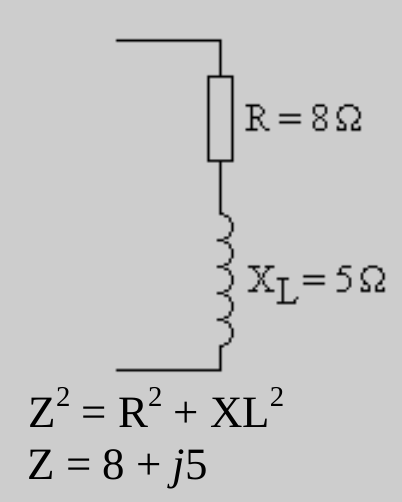
Suponha os seguintes componentes num circuito:
- Um resistor de 3 Ω: representado como 3
- Uma reatância indutiva de 4 Ω: representada como j4
A impedância total é: Z=3+j4
Esse número complexo descreve a combinação da oposição resistiva e reativa ao fluxo de corrente alternada.
Agora, se a reatância fosse capacitiva de -4 Ω, a impedância seria: Z=3−j4
Operações com Números Complexos: Soma, Produto, Divisão e Mais
I. Adição e Subtração
Na forma retangular, somar ou subtrair dois números complexos é extremamente direto: basta somar (ou subtrair) separadamente as partes reais e as partes imaginárias.
Fórmula Geral:
\[(a + jb) \pm (c + jd) = (a \pm c) + j(b \pm d)\]
Exemplos:
- \((9 + j5) + (3 + j2) = (9 + 3) + j(5 + 2) = 12 + j7\)
- \((9 + j5) – (3 – j2) = (9 – 3) + j(5 + 2) = 6 + j7\)
Essas operações são úteis, por exemplo, ao somar impedâncias em série em um circuito AC.
II. Multiplicação por Números Reais
Multiplicar um número complexo por um número real afeta tanto a parte real quanto a imaginária proporcionalmente: k⋅(a+jb)=ka+j(kb)k \cdot (a + jb) = ka + j(kb)
Exemplos:
- \(4 \cdot j3 = j12\)
- \(1.5 \cdot j2 = j3\)
- \(-2 \cdot (3 + j4) = -6 – j8\)
Isso frequentemente ocorre em simulações ou cálculos de potência, onde se escala uma impedância ou corrente complexa por um fator de tensão.
III. Multiplicação de Termos Imaginários
Multiplicar dois termos puramente imaginários nos leva à propriedade fundamental: \[j \cdot j = j^2 = -1\]
Exemplo:
\[3 \cdot j4 = (3 \cdot 4) \cdot j^2 = 12 \cdot (-1) = -12\]
Esse tipo de multiplicação aparece ao resolver produtos vetoriais ou calcular potência reativa.
IV. Multiplicação de Números Complexos Completos
Usa-se a propriedade distributiva (como no produto notável da álgebra):
Fórmula:
\[(a + jb)(c + jd) = ac + ajd + jbc + j^2bd = (ac – bd) + j(ad + bc)\]
Exemplo:
\[9 + j5)(3 – j2) = 27 – j18 + j15 – j^2(10) = 27 – j3 + 10 = 37 – j3\]
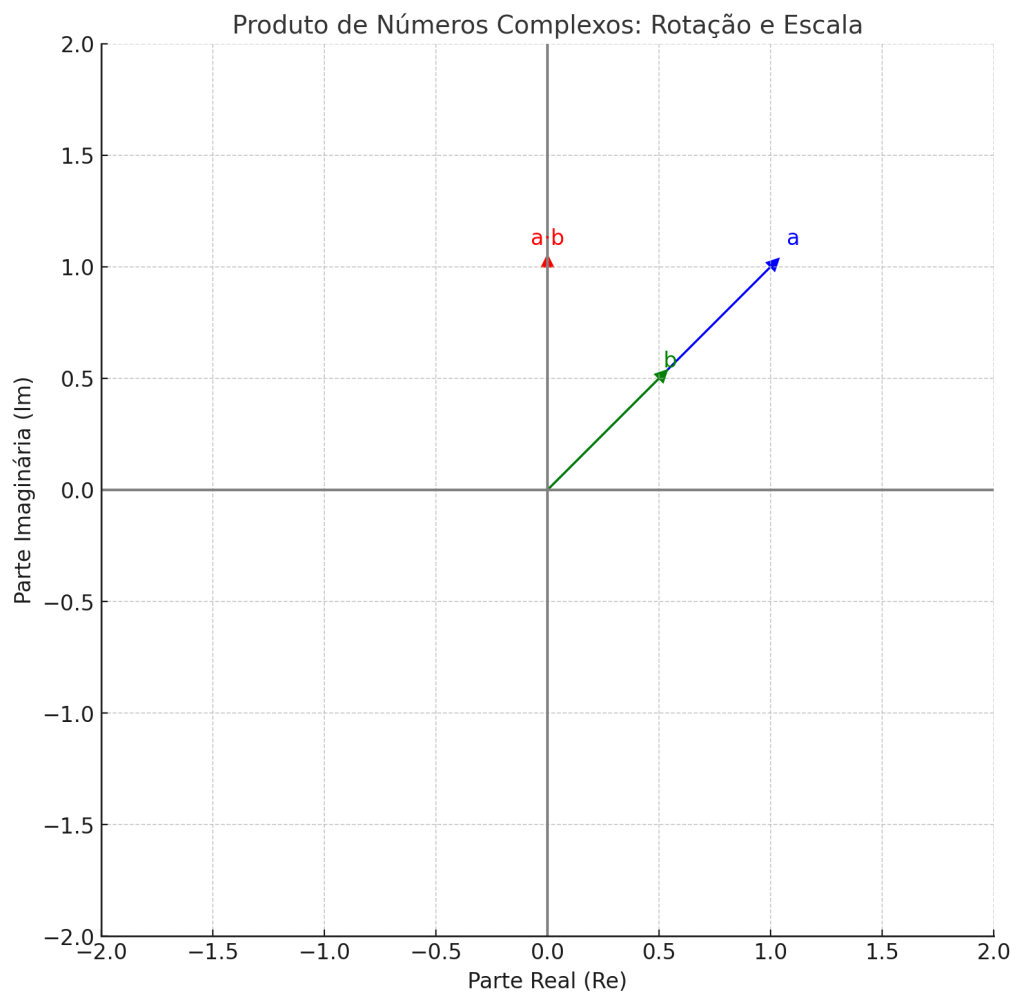
Essa operação é fundamental, por exemplo, na multiplicação de fasores em simulações de sinais AC em linguagem Python usando bibliotecas como NumPy.
V. Divisão de Números Complexos
1. Quando o divisor é um número real:
\[\frac{a + jb}{k} = \frac{a}{k} + j\frac{b}{k}\]
2. Quando o divisor é um número imaginário:
\[\frac{j30}{j5} = \frac{30}{5} = 6\]
Pois jj=1\frac{j}{j} = 1
3. Quando o divisor é um número complexo:
É necessário racionalizar o denominador, multiplicando numerador e denominador pelo conjugado do denominador: \[\frac{4}{1 + j2} \cdot \frac{1 – j2}{1 – j2} = \frac{4(1 – j2)}{(1 + j2)(1 – j2)} =4−j81−j2(4)=4−j81+4=4−j85=0,8−j1,6= \frac{4 – j8}{1 – j^2(4)} = \frac{4 – j8}{1 + 4} = \frac{4 – j8}{5} = 0,8 – j1,6\]
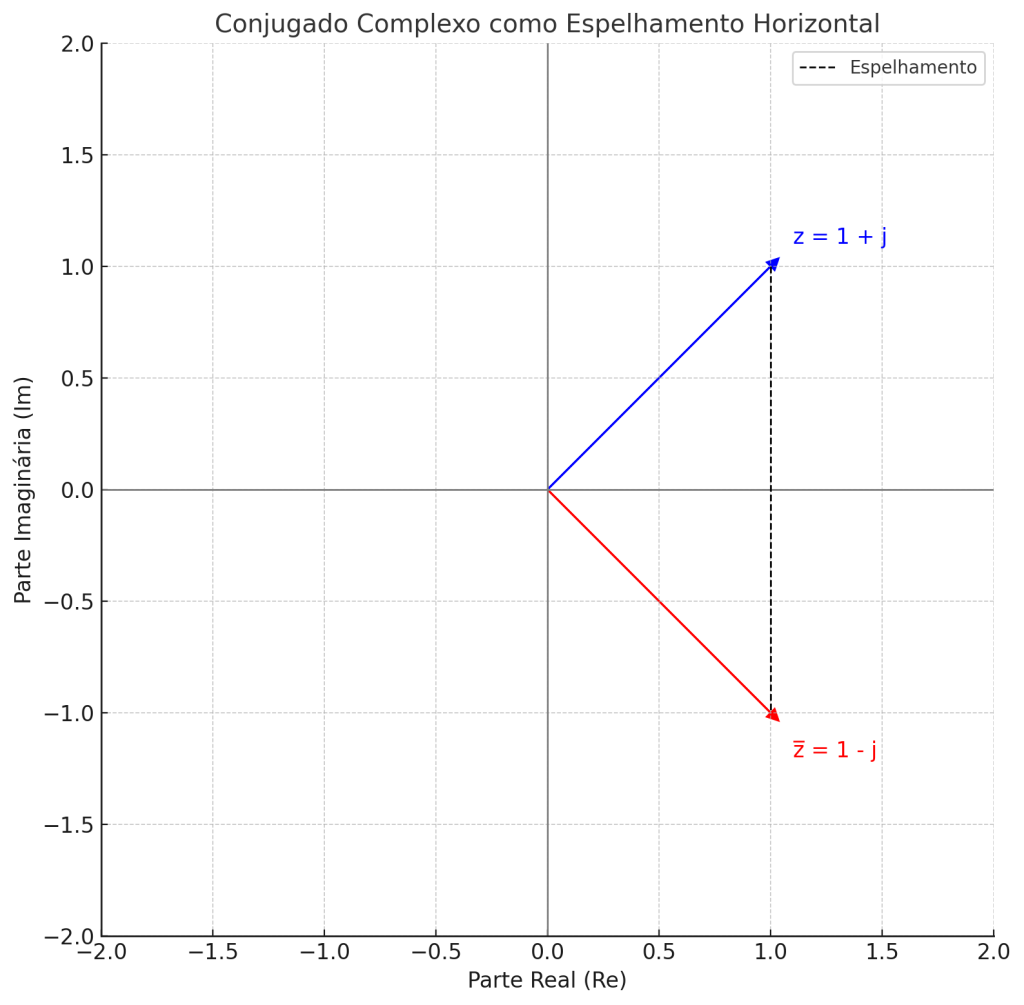
Essa racionalização é uma técnica comum em algoritmos de controle vetorial e manipulação de sinais no domínio da frequência.
Conversão Entre Formas Retangular e Polar
A forma retangular expressa um número complexo como \[z = a + jb\], ou seja, a soma de uma parte real e uma parte imaginária. Já a forma polar expressa o mesmo número com sua magnitude (módulo) e fase (ângulo), da forma: \[z = |z|\angle \theta\]
onde:
- |z| é o módulo do número complexo, ou seja, sua distância até a origem no plano complexo;
- θ é o ângulo de fase (em graus ou radianos), indicando a inclinação do vetor em relação ao eixo real.
I. Retangular → Polar
Fórmulas:
\[|z| = \sqrt{a^2 + b^2} θ=arctan(ba)\theta = \arctan\left(\frac{b}{a}\right)\]
Observações:
- Se a<0a < 0, pode ser necessário ajustar o ângulo para o quadrante correto (ex.: somar 180°);
- Se a=0a = 0, o ângulo será exatamente ±90°, dependendo do sinal de bb.
Exemplo 1:
\[|z| = \sqrt{2^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} ≈ 4,47 θ=arctan(42)=arctan(2)≈63,4°\theta = \arctan\left(\frac{4}{2}\right) = \arctan(2) ≈ 63,4°\]
Portanto: \[z = 4,47\angle 63,4°\]
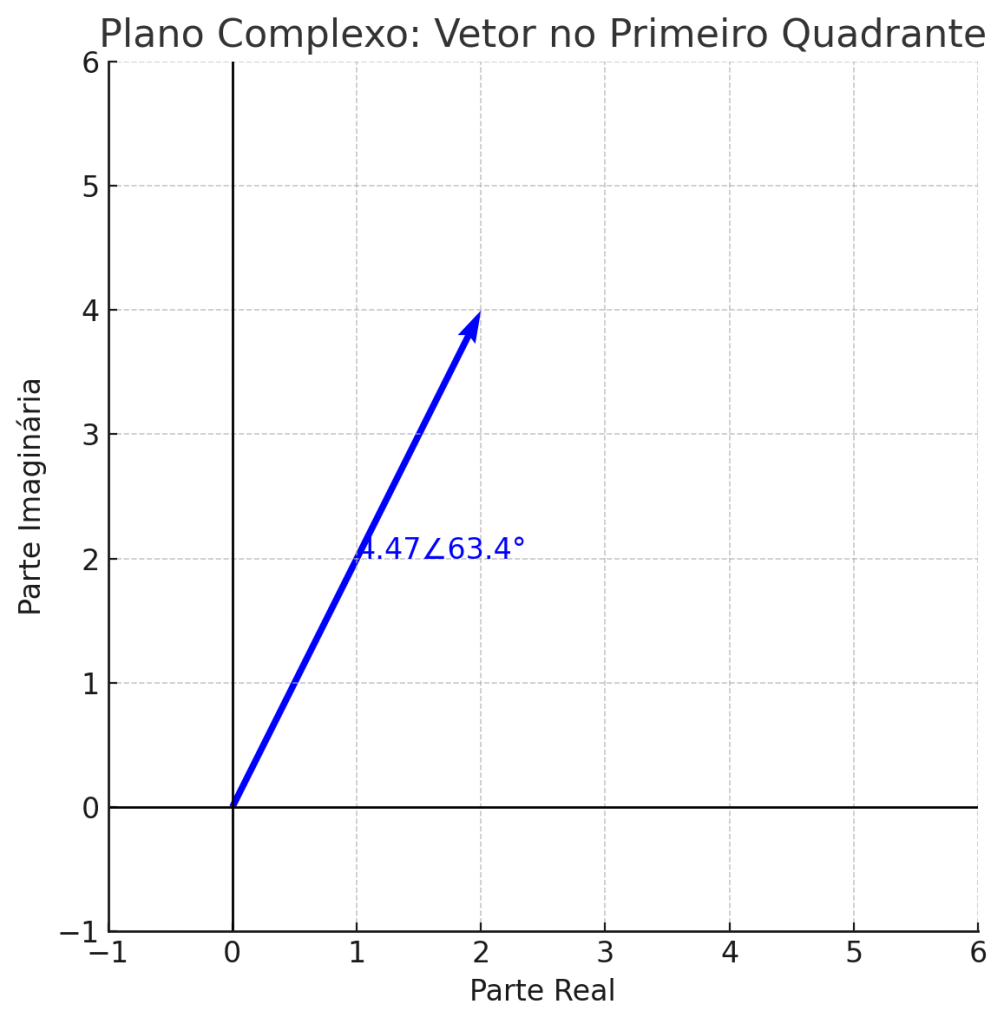
Exemplo 2:
\[|z| = \sqrt{4^2 + (-4)^2} = \sqrt{32} ≈ 5,66 θ=arctan(−44)=−45°\theta = \arctan\left(\frac{-4}{4}\right) = -45°\]
Logo: \[z = 5,66\angle -45°\]
II. Polar → Retangular
Agora o processo é inverso. Se temos a magnitude e o ângulo, podemos obter a forma retangular: \[a = |z| \cdot \cos(\theta) b=∣z∣⋅sin(θ)b = |z| \cdot \sin(\theta)\]
Exemplo:
\[a = 12 \cdot \cos(65°) ≈ 12 \cdot 0,423 = 5,08\] \[b=12⋅sin(65°)≈12⋅0,906=10,87\]\[b = 12 \cdot \sin(65°) ≈ 12 \cdot 0,906 = 10,87\\]
Resultado: \[z = 5,08 + j10,87\]
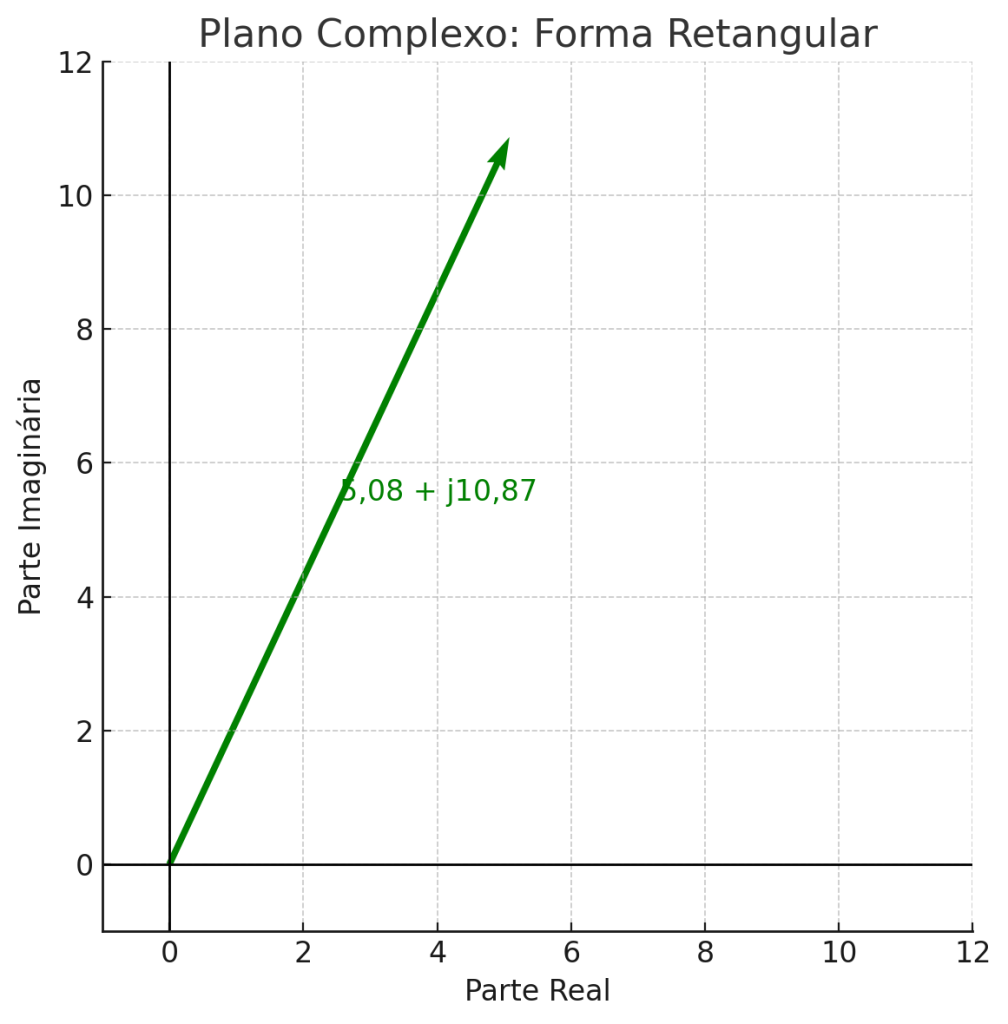
Essa conversão entre formas é amplamente usada em sistemas de potência para transformar medições de corrente e tensão em análise vetorial, e em programação quando se utiliza bibliotecas como cmath (Python) ou std::complex (C++) que operam naturalmente com ângulos e módulos.
Operações com Números Complexos na Forma Polar
Uma das grandes vantagens de representar números complexos em forma polar é a simplicidade com que multiplicações e divisões são realizadas. Em vez de aplicar regras distributivas e lidar com j2=−1j^2 = -1, basta multiplicar os módulos e somar ou subtrair os ângulos, o que é muito mais prático em engenharia e programação.
I. Multiplicação na Forma Polar
Dado dois números complexos: \[z_1 = |z_1|\angle \theta_1 \quad \text{e} \quad z_2 = |z_2|\angle \theta_2\]
A multiplicação é feita por: \[z_1 \cdot z_2 = |z_1||z_2|\angle (\theta_1 + \theta_2)\]
Exemplo:
\[z_1 = 3\angle 45^\circ, \quad z_2 = 2\angle 30^\circ z=3⋅2∠(45∘+30∘)=6∠75∘z = 3 \cdot 2 \angle (45^\circ + 30^\circ) = 6 \angle 75^\circ\]
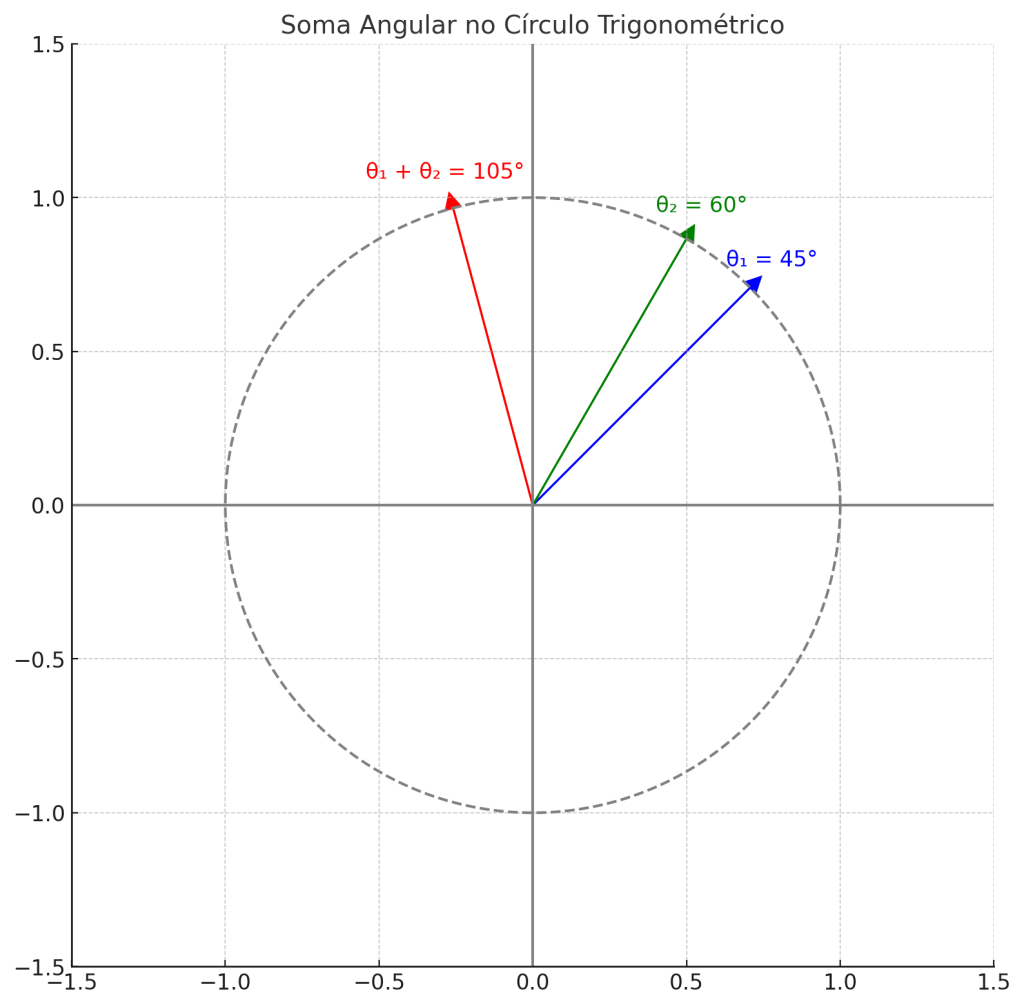
Essa propriedade é amplamente utilizada na multiplicação de fasores em análise de corrente alternada (AC), onde cada grandeza possui fase distinta.
II. Divisão na Forma Polar
De forma análoga à multiplicação, a divisão segue: \[\frac{z_1}{z_2} = \frac{|z_1|}{|z_2|}\angle (\theta_1 – \theta_2)\]
Exemplo:
\[z_1 = 10\angle 60^\circ, \quad z_2 = 2\angle 30^\circ z1z2=102∠(60∘−30∘)=5∠30∘\frac{z_1}{z_2} = \frac{10}{2} \angle (60^\circ – 30^\circ) = 5 \angle 30^\circ\]
Essa operação é comum em controle vetorial de motores e análise de filtros, onde precisamos determinar a relação entre sinais com módulos e fases diferentes.
III. Casos Mistos: Real × Polar e Real ÷ Polar
Se um número real é multiplicado por um número complexo em forma polar, o resultado é simplesmente a multiplicação dos módulos — o ângulo permanece: k⋅∣z∣∠θ=(k∣z∣)∠θk \cdot |z|\angle \theta = (k|z|)\angle \theta
Se um número real for dividido por um número complexo polar, precisamos aplicar: \[\frac{k}{|z|\angle \theta} = \frac{k}{|z|} \angle -\theta\]
Exemplo:
\[\frac{10}{5\angle 60^\circ} = 2 \angle -60^\circ\]
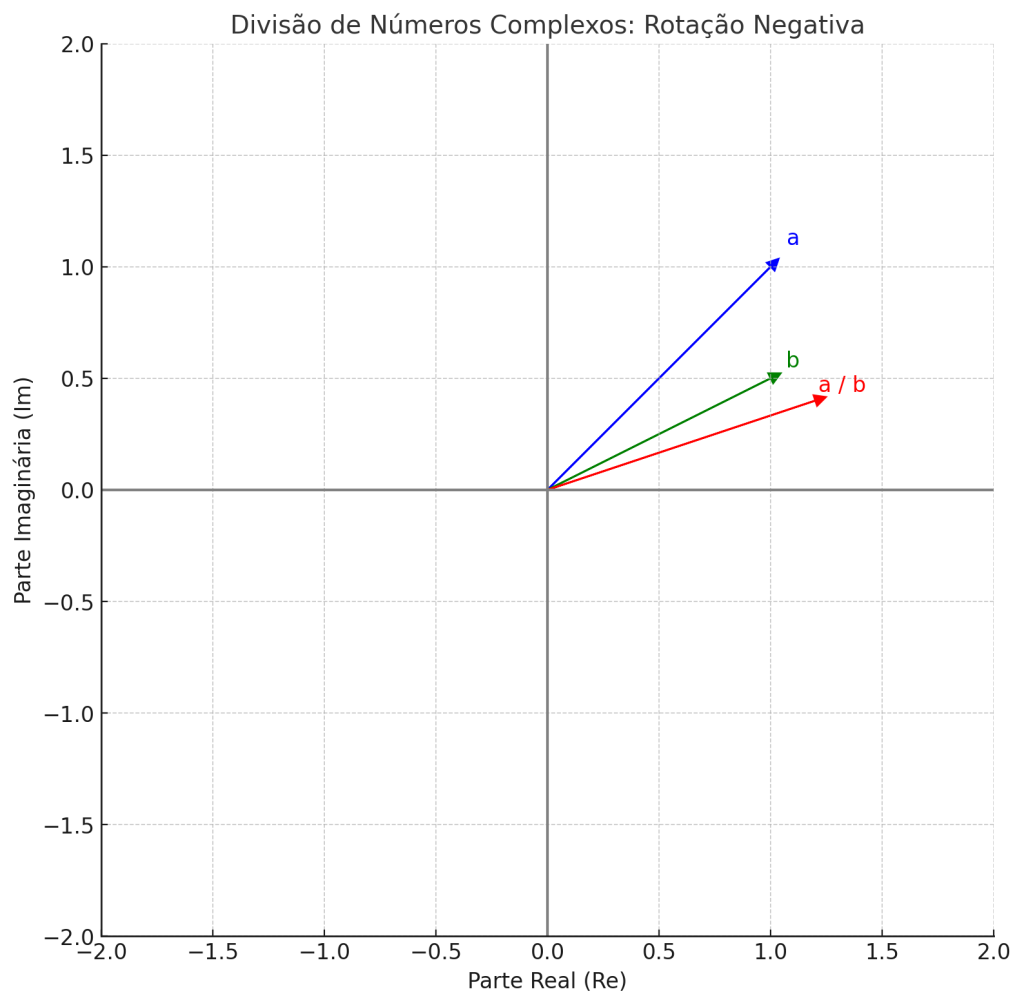
Essas simplificações mostram como a forma polar dos números complexos se alinha naturalmente com as propriedades trigonométricas dos sinais senoidais. Em programação, especialmente em linguagens como Python ou MATLAB, essas operações podem ser feitas usando bibliotecas com suporte direto à forma polar, como cmath.polar() e cmath.rect().
Aplicando Números Complexos na Resolução de Circuitos AC
A análise de circuitos de corrente alternada exige mais do que apenas resistências: capacitores e indutores introduzem defasagens e reatâncias que variam com a frequência. A forma mais elegante e eficiente de lidar com esses fenômenos é usar números complexos para representar as impedâncias.
I. Impedância em Forma Complexa
Lembre-se de que:
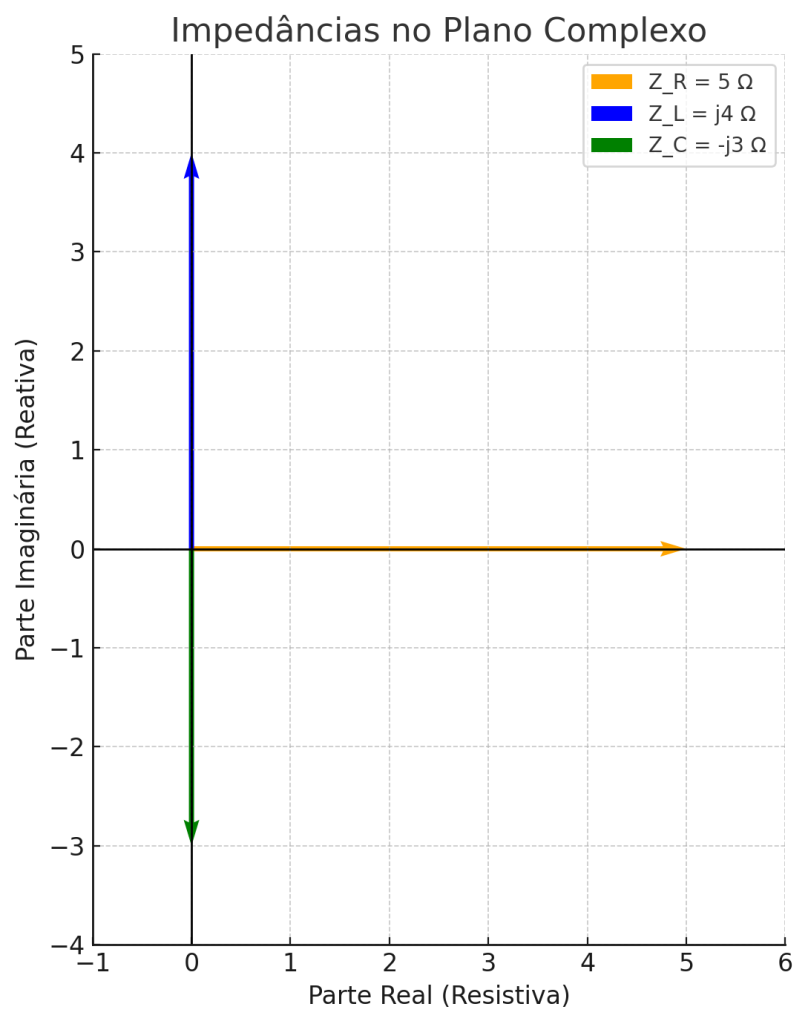
- Um resistor possui impedância puramente real: \(Z_R = R\)
- Um indutor possui impedância puramente imaginária positiva: \(Z_L = jX_L = j\omega L\]
- Um capacitor possui impedância puramente imaginária negativa: \(Z_C = -jX_C = -j \cdot \frac{1}{\omega C}\)
Sendo \(\omega = 2\pi\) f, a frequência angular da fonte senoidal.
II. Circuito com Componentes em Série
Considere um circuito com os seguintes componentes:
- R=3 Ω
- L=4 Ω de reatância indutiva
A impedância total é: \(Z = R + jX_L = 3 + j4\)
Cálculo da magnitude e ângulo:
\[|Z| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \Omega θ=arctan(43)≈53,1∘\theta = \arctan\left(\frac{4}{3}\right) \approx 53,1^\circ\]
Logo, a impedância pode ser representada como: Z=5∠53,1∘
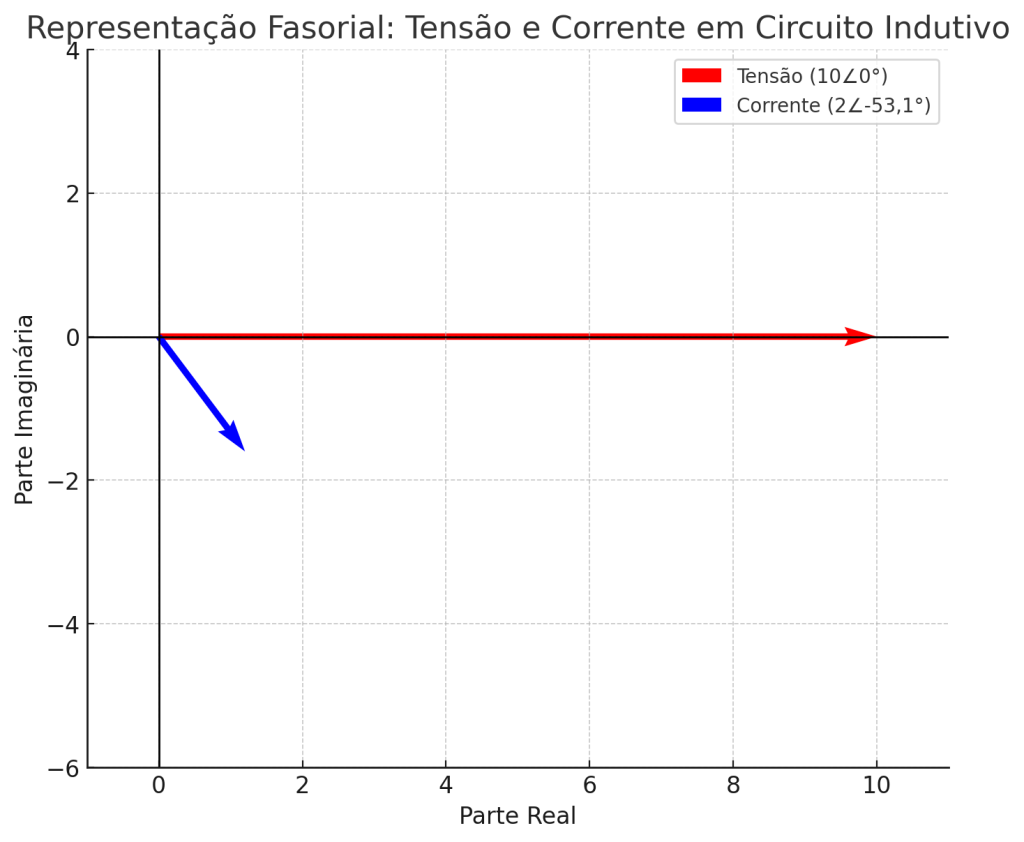
Se a tensão da fonte for V=10∠0∘ V, a corrente no circuito será: \[I = \frac{V}{Z} = \frac{10\angle 0^\circ}{5\angle 53,1^\circ} = 2\angle -53,1^\circ \, \text{A}\]
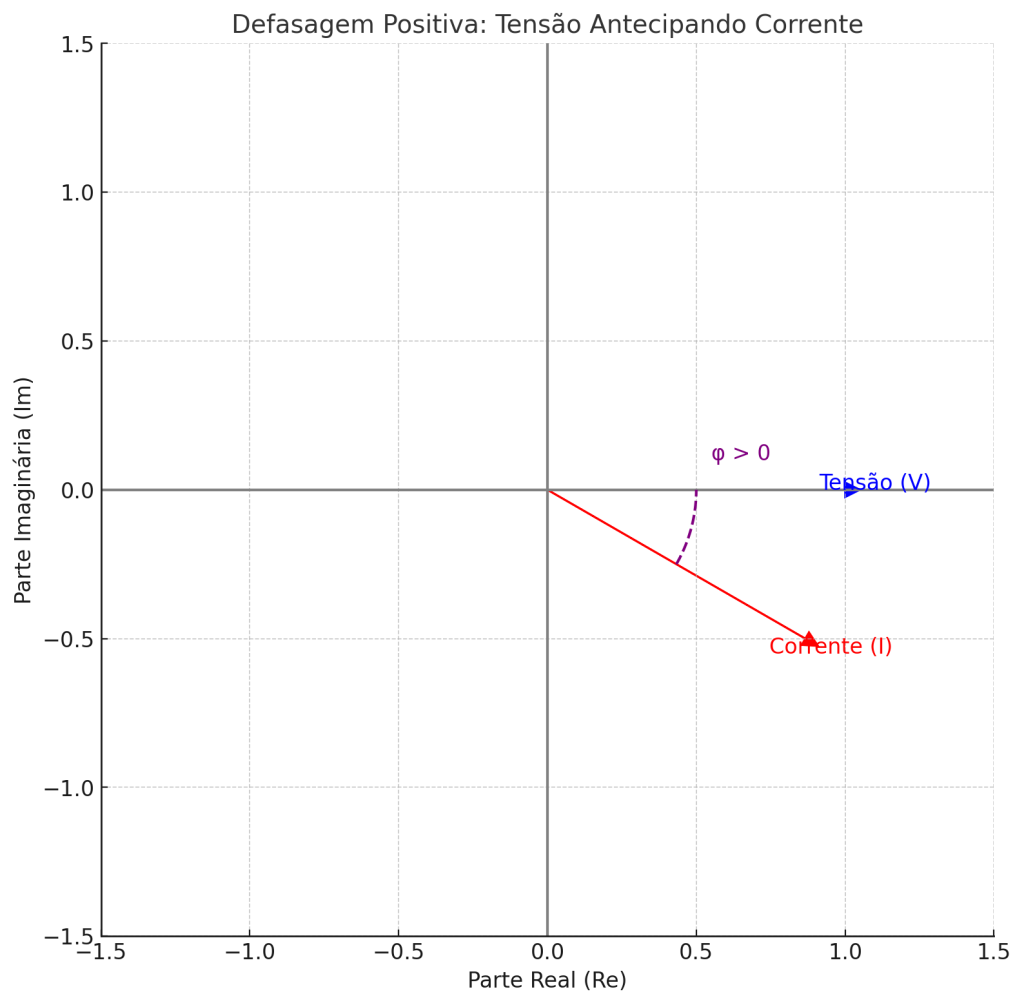
Isso mostra que a corrente está atrasada 53,1° em relação à tensão, devido à presença da indutância.
III. Circuitos com Múltiplos Ramos: Soma de Impedâncias
Para dois ramos em série:
- \(Z_1 = 9 + j6\)
- \(Z_2 = 3 – j2\)
A impedância total é simplesmente: \[Z_T = Z_1 + Z_2 = (9 + 3) + j(6 – 2) = 12 + j4\]
Convertendo para forma polar:
\[|Z_T| = \sqrt{12^2 + 4^2} = \sqrt{144 + 16} = \sqrt{160} \approx 12,65 θ=arctan(412)≈18,4∘\theta = \arctan\left(\frac{4}{12}\right) \approx 18,4^\circ\]
Portanto: \[Z_T = 12,65\angle 18,4^\circ\]
IV. Circuitos com Impedâncias em Paralelo
Neste caso, o uso de números complexos exige a soma de inversos, pois: \[\frac{1}{Z_{eq}} = \frac{1}{Z_1} + \frac{1}{Z_2}\]
Exemplo:
- \(Z_1 = 8 + j5\)
- \(Z_2 = 10 – j6\)
Calcular diretamente a impedância equivalente exigirá conversão para forma polar, inversão e nova soma, ou uso de produto sobre soma se forem apenas dois ramos: \[Z_{eq} = \frac{Z_1 \cdot Z_2}{Z_1 + Z_2}\]
Essa técnica é extremamente útil em programação, pois você pode encapsular essa lógica em uma função para reutilização em análise de topologias mais complexas.
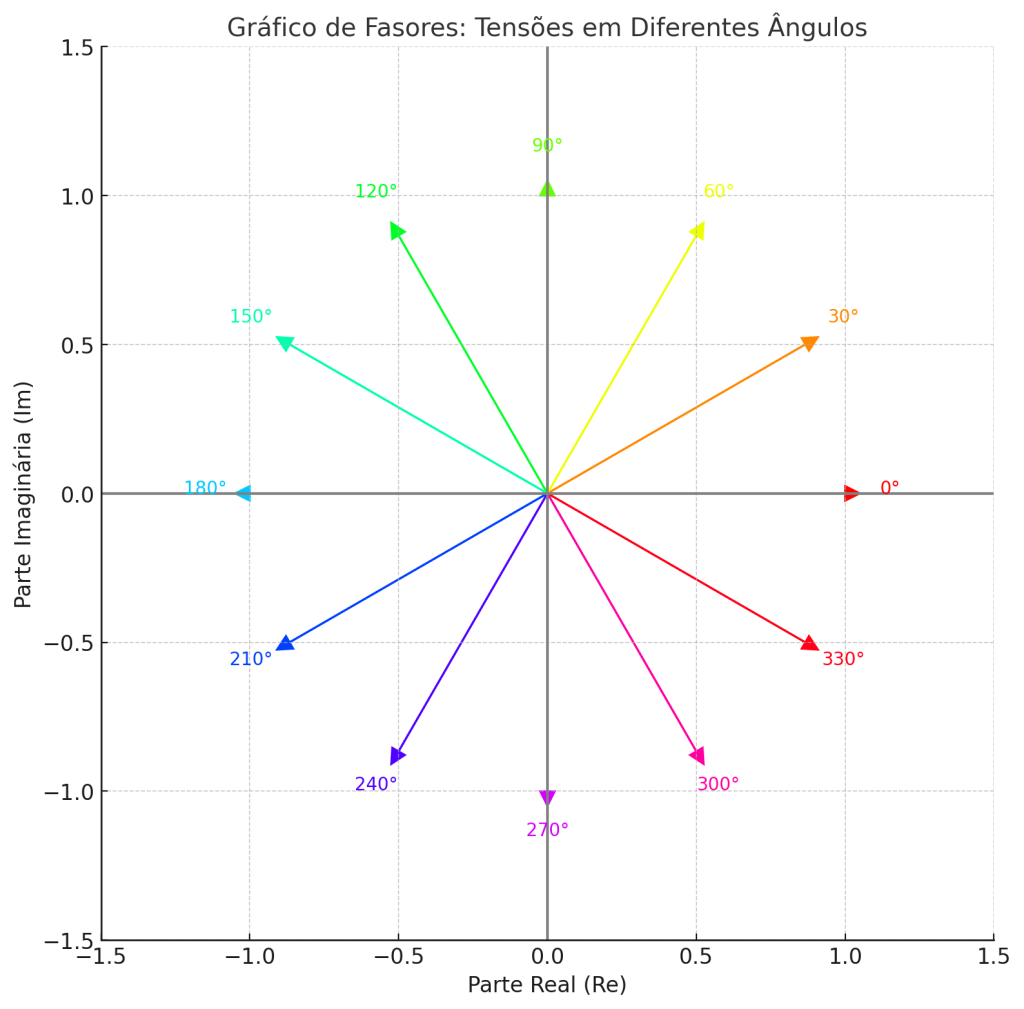
Análise de Tensões e Representação Fasorial
Vamos considerar um circuito com os seguintes componentes ligados em série:
- \(R_1 = 2 \, \Omega\)
- \(L = j4 \, \Omega\)
- \(R_2 = 4 \, \Omega\)
- \(C = -j12 \, \Omega\)
A tensão total aplicada ao circuito é \(V_T = 100 \angle 0^\circ \, \text{V}\)
1) Impedância Total
Somamos as impedâncias: \[Z_T = R_1 + j4 + R_2 – j12 = (2 + 4) + j(4 – 12) = 6 – j8 \, \Omega\]
Módulo e ângulo:
\[|Z_T| = \sqrt{6^2 + (-8)^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \, \Omega θ=arctan(−86)=−53,13∘\theta = \arctan\left(\frac{-8}{6}\right) = -53,13^\circ\]
2) Corrente Total
\[I_T = \frac{V_T}{Z_T} = \frac{100\angle 0^\circ}{10\angle -53,13^\circ} = 10 \angle 53,13^\circ \, \text{A}\]
Note que a corrente está atrasada em relação à tensão total devido à predominância capacitiva no circuito.
3) Tensões em Cada Componente
A corrente é a mesma em todos os elementos (circuito em série), então podemos calcular:
Tensão em \(R_1\):
\[V_{R1} = R_1 \cdot I_T = 2 \cdot 10\angle -53,13^\circ = 20 \angle -53,13^\circ \, \text{V}\]
Tensão no indutor L:
\[V_L = j4 \cdot 10\angle -53,13^\circ = 40 \angle (90^\circ – 53,13^\circ) = 40 \angle 36,87^\circ\]
Tensão no capacitor CC:
\[V_C = (-j12) \cdot 10\angle -53,13^\circ = 120 \angle (-90^\circ – 53,13^\circ) = 120 \angle -143,13^\circ\]
Tensão em \[R_2:\]
\[V_{R2} = 4 \cdot 10\angle -53,13^\circ = 40 \angle -53,13^\circ \, \text{V}\]
4) Soma Vetorial das Tensões
Vamos converter todas as tensões para a forma retangular para somar:
- \[V_{R1} = 20 \cdot \cos(-53,13^\circ) + j \cdot 20 \cdot \sin(-53,13^\circ) ≈ 12 + j(-16)\]
- \[V_L ≈ 40 \cdot \cos(36,87^\circ) + j \cdot 40 \cdot \sin(36,87^\circ) ≈ 32 + j24\]
- \[V_{R2} ≈ 40 \cdot \cos(-53,13^\circ) + j \cdot 40 \cdot \sin(-53,13^\circ) ≈ 24 + j(-32)\]
- \[V_C ≈ 120 \cdot \cos(-143,13^\circ) + j \cdot 120 \cdot \sin(-143,13^\circ) ≈ -96 + j(-72)\]
Somando: \[V_T ≈ (12 + 32 + 24 – 96) + j(-16 + 24 – 32 – 72) = (-28) + j(-96) ∣VT∣≈(−28)2+(−96)2≈784+9216=10000=100 V|V_T| ≈ \sqrt{(-28)^2 + (-96)^2} ≈ \sqrt{784 + 9216} = \sqrt{10000} = 100 \, \text{V} θ=arctan(−96−28)≈−106,3∘\theta = \arctan\left(\frac{-96}{-28}\right) ≈ -106,3^\circ\]
No entanto, como essa fase representa um sistema completo com cancelamentos parciais, a soma vetorial das tensões confirma o valor total da fonte, o que valida todos os cálculos.
5) Observações Fasoriais
- A tensão no capacitor atrasou 143,13° em relação à fonte.
- A tensão no indutor adiantou 36,87°.
- As resistências mantêm-se em fase com a corrente.
- A diferença angular entre \(V_C\) e \(V_L\) é de aproximadamente 180°, evidenciando que indutores e capacitores se opõem em fase.
Modelos de Impedância em Circuitos AC: RC, RL, LC e RLC
Os circuitos AC mais comuns são compostos por combinações de resistores (R), capacitores (C) e indutores (L). Usando números complexos, podemos expressar a impedância total desses circuitos com precisão e facilidade.
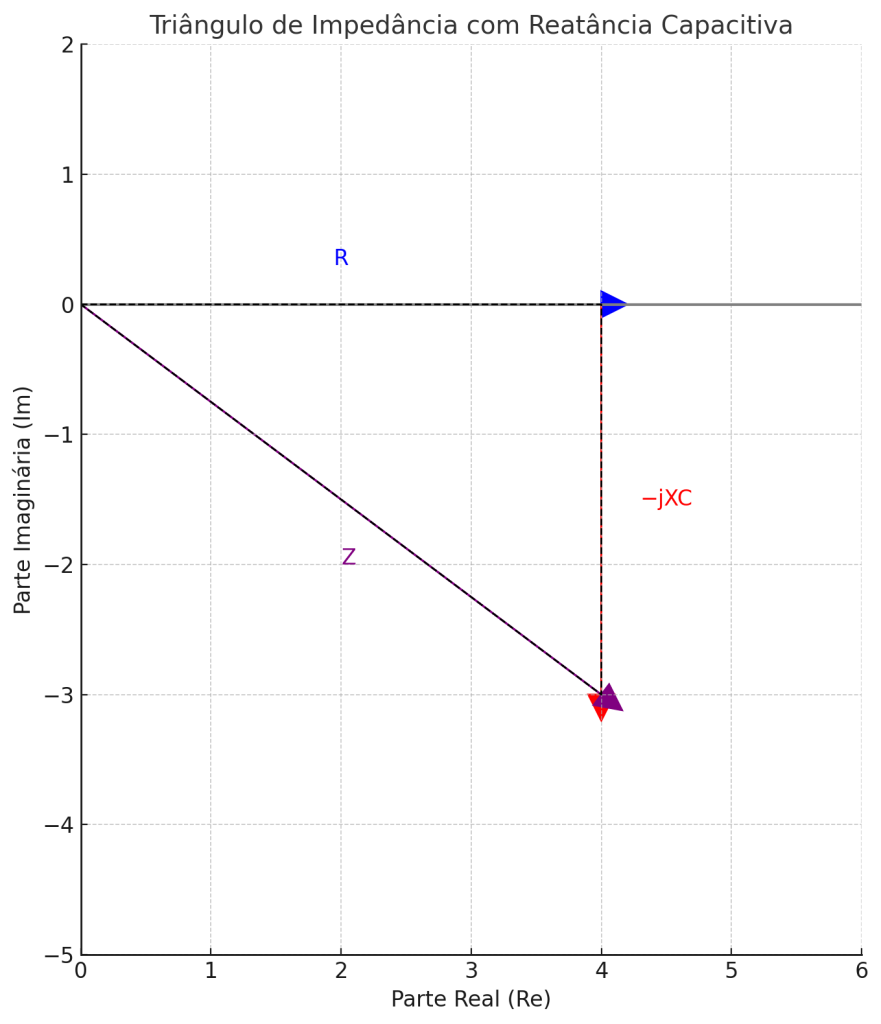
1. Circuito RC Série
Componentes: Resistor RR e capacitor CC
Impedância Total:
\[Z = R – jX_C = R – j\left(\frac{1}{\omega C}\right)\]
Módulo e ângulo:
\[|Z| = \sqrt{R^2 + X_C^2} θ=−arctan(XCR)\theta = -\arctan\left(\frac{X_C}{R}\right)\]
Exemplo de uso:
- Filtros passa-baixa analógicos
- Circuitos de retardo de fase
- Temporizações com constantes de tempo τ=RC\tau = RC
2. Circuito RL Série
Componentes: Resistor RR e indutor LL
Impedância Total:
\[Z = R + jX_L = R + j\omega L\]
Módulo e ângulo:
\|Z| = \sqrt{R^2 + X_L^2} θ=arctan(XLR)\theta = \arctan\left(\frac{X_L}{R}\right)\]
Aplicações típicas:
- Controle de motores AC
- Filtros passa-altas
- Correção de fator de potência indutivo
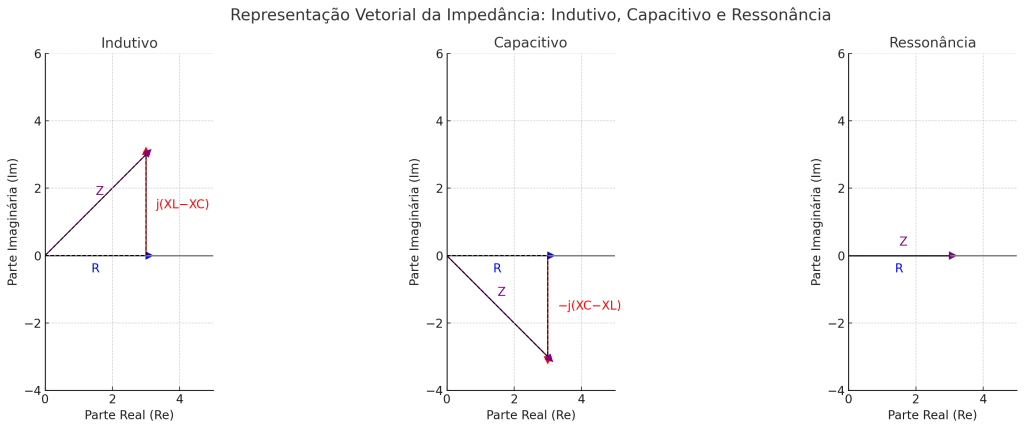
3. Circuito LC Série
Componentes: Indutor e capacitor, sem resistência
Impedância Total:
\[Z = jX_L – jX_C = j(X_L – X_C)\]
Observações:
- Quando \(X_L = X_C\), temos ressonância: \(Z = 0 \quad \text{(curto para corrente AC em frequência ressonante)}\)
- Quando \(X_L > X_C\): circuito é indutivo
- Quando XC>XLX_C > X_L: circuito é capacitivo
Aplicações:
- Filtros ressonantes
- Circuitos sintonizados
- Osciladores LC
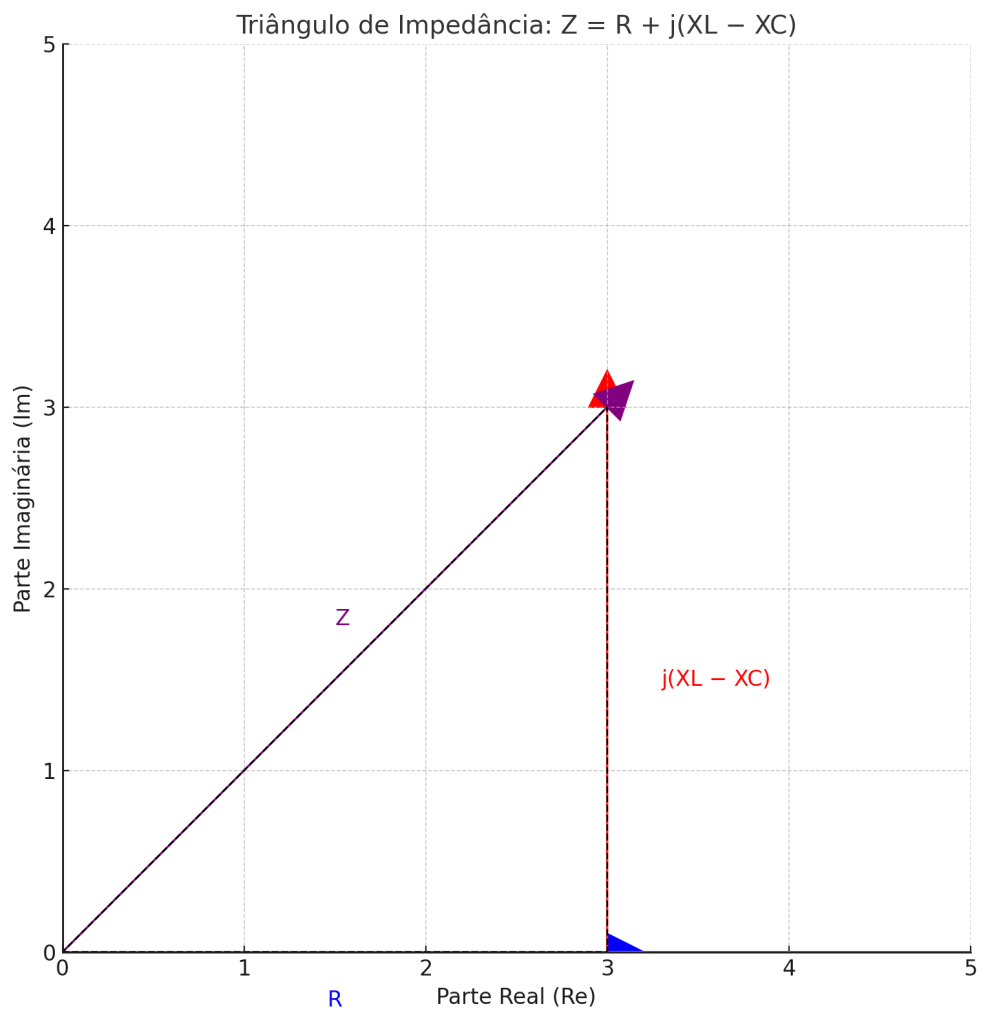
4. Circuito RLC Série
Componentes: R, L e C
Impedância Total:
\[Z = R + j(X_L – X_C)\]
Módulo e ângulo:
\[|Z| = \sqrt{R^2 + (X_L – X_C)^2} θ=arctan(XL−XCR)\theta = \arctan\left(\frac{X_L – X_C}{R}\right)\]
Fator de qualidade (Q):
\[Q = \frac{X_L}{R} = \frac{\omega L}{R} \quad \text{(ou equivalente com C)}\]
Aplicações:
- Filtros de banda estreita (passa-banda)
- Equalizadores
- Ressonância em RF
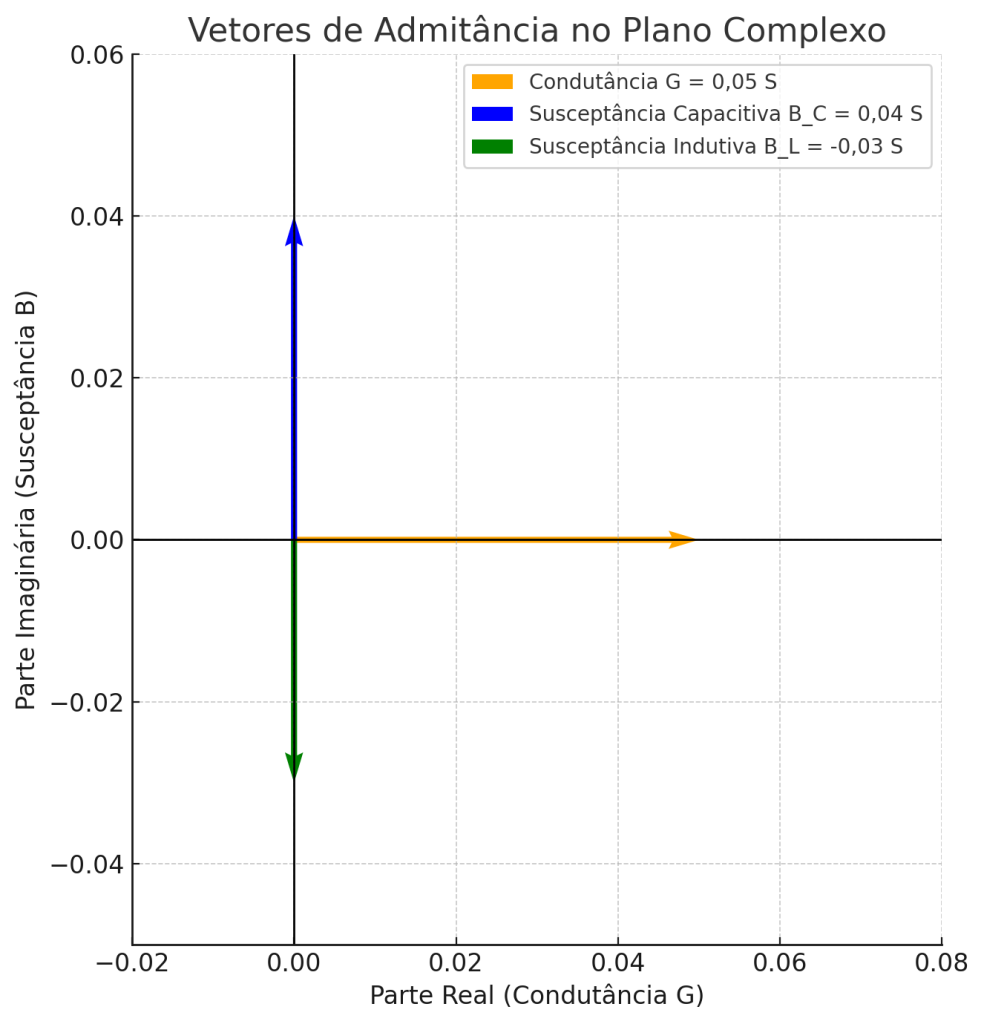
5. Circuito RLC Paralelo
Fórmula geral da impedância:
\[\frac{1}{Z} = \frac{1}{R} + \frac{1}{jX_L} + \frac{1}{-jX_C}\]
Ou utilizando Y = 1/Z (admitância), pode-se somar diretamente:
- Parte real: G=1/RG = 1/R
- Parte imaginária: B=1XC−1XLB = \frac{1}{X_C} – \frac{1}{X_L}
Módulo da admitância:
\[|Y| = \sqrt{G^2 + B^2} \quad \Rightarrow \quad Z = \frac{1}{|Y|}\]
Ângulo da impedância:
\[\theta = -\arctan\left(\frac{B}{G}\right)\]
Aplicações:
- Rejeição de banda
- Estabilização de sistemas oscilatórios
- Sintonização paralela
Essas representações facilitam o cálculo algébrico e a simulação computacional. Em ambientes como Python com numpy e matplotlib, ou MATLAB, podemos montar funções que calculam e ploteiam o comportamento desses circuitos com base em frequência, fornecendo insights valiosos sobre resposta de fase, magnitude e potência.
Excelente! Para finalizar nosso artigo, abordaremos um dos tópicos mais práticos e importantes em eletrônica de potência e sistemas de energia: a potência em circuitos AC, e como os números complexos nos ajudam a entender as relações entre potência real (ativa), reativa e aparente, além do fator de potência, fundamental para eficiência energética.
Potência em Circuitos AC: Ativa, Reativa, Aparente e Fator de Potência
Diferente de circuitos em corrente contínua (DC), nos circuitos de corrente alternada (AC) a potência elétrica se divide em três componentes:
I. Potência Aparente (S)
Representa a potência total fornecida pela fonte. É um número complexo e tem unidade em volt-ampère (VA). \[S = V \cdot I^* = |V| \cdot |I| \angle(\theta_V – \theta_I)\]
Onde:
- V é a tensão em forma complexa (fasor),
- \(I^*\) é o conjugado da corrente,
- θ é a defasagem entre tensão e corrente.
Módulo:
\[|S| = V \cdot I\]
II. Potência Ativa ou Real (P)
É a potência efetivamente consumida por cargas resistivas, convertida em trabalho (calor, luz, movimento etc.). É a parte real de S: \[P = V \cdot I \cdot \cos\theta \quad \text{(Watts, W)}\]
III. Potência Reativa (Q)
É a potência que circula entre a fonte e os elementos reativos (indutores e capacitores), mas não realiza trabalho. É a parte imaginária de S: \[Q = V \cdot I \cdot \sin\theta \quad \text{(VAr, Volt-Ampère Reativo)}\]
IV. Relação Vetorial: Triângulo de Potência
A relação entre as três potências forma um triângulo no plano complexo: \(S = P + jQ\] [Inserir diagrama com triângulo de potência: P na horizontal, Q na vertical, S como hipotenusa]
V. Fator de Potência (FP)
O fator de potência indica o quanto da potência aparente está sendo aproveitada para trabalho real: \[\text{FP} = \cos\theta = \frac{P}{|S|}\]
- FP = 1 → 100% da potência está sendo usada (ideal)
- FP baixo → muita potência reativa, baixa eficiência
Alternativas de cálculo:
\[\theta = \arctan\left(\frac{Q}{P}\right) \quad \text{ou} \quad FP = \frac{R}{|Z|}\]
VI. Correção do Fator de Potência
Quando o fator de potência é baixo (muito atraso ou avanço entre corrente e tensão), usam-se capacitores ou indutores para correção, dependendo do caso:
- Se FP indutivo (corrente atrasada): adiciona-se capacitores
- Se FP capacitivo (corrente adiantada): adiciona-se indutores
Isso é especialmente importante em sistemas industriais e em dimensionamento de fontes chaveadas, onde se busca reduzir perdas e custos operacionais.
VII. Aplicação em Programação e Simulação
Em códigos Python ou MATLAB, podemos calcular as três potências a partir dos fasores complexos:
import cmath
V = 220 * cmath.rect(1, 0) # Tensão 220∠0°
I = 10 * cmath.rect(1, -0.785) # Corrente 10∠-45° (atrasada)
S = V * I.conjugate()
P = S.real
Q = S.imag
FP = P / abs(S)
Esse tipo de cálculo é comum em bibliotecas de simulação elétrica, e também em firmware embarcado com DSPs para controle de inversores e fontes.
Perfeito. Vamos agora à seção final do artigo.
Conclusão: Por que Dominar Números Complexos é Essencial para Engenharia e Programação
Os números complexos não são apenas uma curiosidade matemática — eles formam a espinha dorsal da análise de sistemas em corrente alternada, sinais oscilatórios, filtros, motores, fontes chaveadas, redes de comunicação, e uma infinidade de aplicações que exigem modelagem precisa de grandezas que oscilam com magnitude e fase.
Ao longo deste artigo, vimos como a forma retangular dos números complexos nos permite:
- Representar impedâncias com componentes resistivos e reativos;
- Somar tensões e correntes de maneira vetorial;
- Traduzir circuitos reais em modelos matemáticos manipuláveis.
Vimos também como a forma polar:
- Facilita multiplicações e divisões entre fasores;
- Permite interpretar intuitivamente a defasagem entre sinais;
- Se conecta diretamente com a potência aparente, essencial para o dimensionamento de fontes e correção de fator de potência.
Além disso, usamos gráficos e ferramentas computacionais com Python para visualizar vetores no plano complexo, admitâncias, fasores e triângulos de potência — transformando a matemática em uma linguagem visual e prática.
Para o programador:
Entender números complexos te capacita a trabalhar com algoritmos de controle vetorial, análise de Fourier, filtros digitais (IIR, FIR), demoduladores e equalizadores.
Para o engenheiro eletrônico:
É impossível projetar corretamente um sistema AC ou ressonante sem compreender a relação entre Z, S, P, Q, FP e a geometria vetorial do plano complexo.
Dominar esse conteúdo transforma sua prática profissional: você deixa de apenas “conectar componentes” e passa a modelar, prever e otimizar circuitos com precisão matemática.
Aprender números complexos é como abrir uma nova dimensão da eletrônica — e ela está cheia de possibilidades.
Sobre o Autor
Carlos Delfino
administrator
Um Eterno Aprendiz.
Professor de Introdução a Programação, programação com JavaScript, TypeScript, C/C++ e Python
Professor de Eletrônica Básica
Professor de programação de Microcontroladores.
Embarcatecher
