Para iniciantes, este conceito pode parecer confuso e até inútil. No entanto, para quem deseja trabalhar com microcontroladores, processadores e, principalmente, redes a nível de protocolos, é fundamental compreendê-lo. Mas, afinal, qual o impacto do Big Endian e do Little Endian na transmissão de dados entre sistemas, ou na comunicação entre um módulo e um microcontrolador?
O conceito de Big Endian e Little Endian, denominado simplesmente de Endianness, surgiu com a transição dos computadores de médio porte para os microcomputadores, quando estes passaram a endereçar tanto os bits quanto os bytes de maneira diferente. Esse problema é principalmente observado ao lidar com bytes, pois pode causar embaralhamento de texto, gerando confusão. No caso de tratamento numérico, pode até mesmo comprometer o sistema.
Esse problema começou, como mencionado, quando surgiram os microcomputadores, que adotaram o conceito de Little Endian. Mas o que é Endian? Por que Big ou Little? “Endian” é um termo cunhado a partir de uma história que alude às disputas políticas e religiosas na Europa, descrita em uma obra de ficção escrita por Jonathan Swift em 1726, conhecida em português como *As Viagens de Gulliver*. Na história, dois grupos de cidadãos entram em guerra por não concordarem sobre qual lado do ovo é o correto para se quebrar, o lado maior (Big End) ou o lado menor (Little End), resultando numa guerra civil que separa os grupos.
Na informática, a situação não foi muito diferente. Não houve uma guerra civil, mas os sistemas foram separados em “Big Endian” e “Little Endian”, que definem como os bits são transmitidos em alguns sistemas, e em outros, apenas quando lidamos com palavras (Word/2 bytes, DWord/4 bytes), independentemente de o microprocessador ser de 8 bits ou maior.
Atualmente, não enfrentamos muitos problemas relacionados a esse modo de endereçamento, pois quase todos os microprocessadores usam o Little Endian para endereçar seus dados, com exceção de alguns, como o antigo PowerMAC, que utilizava um PowerPC especial travado em Big Endian. Outros computadores que não usam esse travamento permitem a alternância entre os dois modos no que diz respeito à manipulação dos bytes.
Outras arquiteturas que trabalham com Big Endian incluem a série Motorola 68000 (incluindo Freescale ColdFire), Xilinx Microblaze, SuperH, IBM z/Architecture, Atmel AVR32 e o Intel 8051, com destaque para a instrução `LCALL`, que endereça usando Little Endian.
Mas então, o que é realmente Big Endian e Little Endian?
Como já mencionado, é a forma como os bytes e bits são endereçados na memória. Quando se trata de bytes, o Big Endian endereça, por exemplo, em uma palavra de 2 bytes, o primeiro byte como sendo o endereço menor, e a segunda palavra no endereço seguinte (+1 byte). Já no Little Endian, o segundo byte é endereçado primeiro. Para quem está começando, isso pode causar um certo desconforto, embora as linguagens de programação abstraiam esse problema para nós. Mesmo no C, isso não é perceptível, mas podem surgir problemas ao lidar com ponteiros e estruturas de dados (`struct`), já que o primeiro endereço em um sistema Big Endian não será a menor parte do número, ou seja, a parte menos significativa (LSB), mas sim a parte mais significativa (MSB).
Vejamos abaixo para entender melhor o conceito de *LSB* e *MSB*, que trata da importância do bit ou byte na composição numérica.
**LSB** representa a parte menos significativa do número, ou seja, a parte mais à direita. *Least Significant Bit/Byte*.
Já o **MSB** representa a parte mais significativa, ou seja, a parte mais à esquerda do número. *Most Significant Bit/Byte*.
Agora podemos entender melhor o conceito de Little Endian e Big Endian. Vejamos primeiro, a nível de bits, do que se trata.
Para o **Little Endian**, a representação numérica em bits, onde o algoritmo de conversão numérica que a maioria de nós está acostumada pode ser facilmente representado pela fórmula:
\[
\sum_{i=0}^{N-1} b_i \cdot 2^i
\]
Temos, então, a seguinte ordenação dos bits para a representação do número 180 em Little Endian, onde o bit menos significativo é tratado como sendo o bit 0 e o bit 7 é o bit mais significativo.
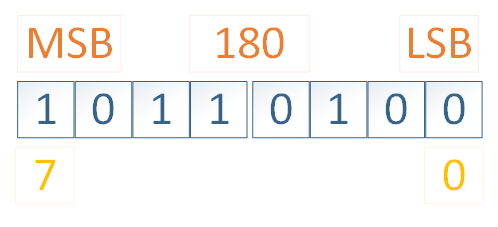
Para o **Big Endian**, os bits mantêm sua disposição, porém sua ordem de transmissão inverte, ou seja, são endereçados do MSB como sendo o primeiro bit, e o LSB como sendo o último bit. Portanto, a fórmula de conversão passa a ser:
\[
\sum_{i=0}^{N-1} b_i \cdot 2^{(N – 1 – i)}
\]
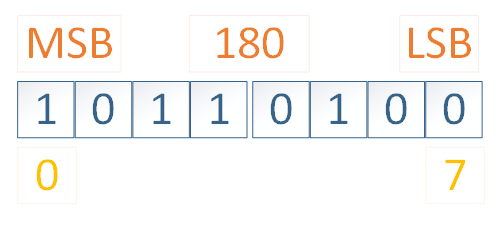
O Conceito de Endianness
No que se refere aos bits, o conceito de **Endianness** afeta mais o hardware no que diz respeito ao endereçamento de memória, à transferência de dados em barramentos, principalmente nos seriais, e às operações de manipulação de bits. Principalmente se formos usar máscaras do tipo *bitwise*, é preciso saber exatamente a ordem dos bits para evitar enganos fatais.
Vejamos agora como é tratado o conceito de **endianness** quando se trata de bytes, o que afeta mais a manipulação do dado na memória, quando é representado com mais de dois bytes, como em números *inteiros* e *short int* em máquinas de 32 bits.
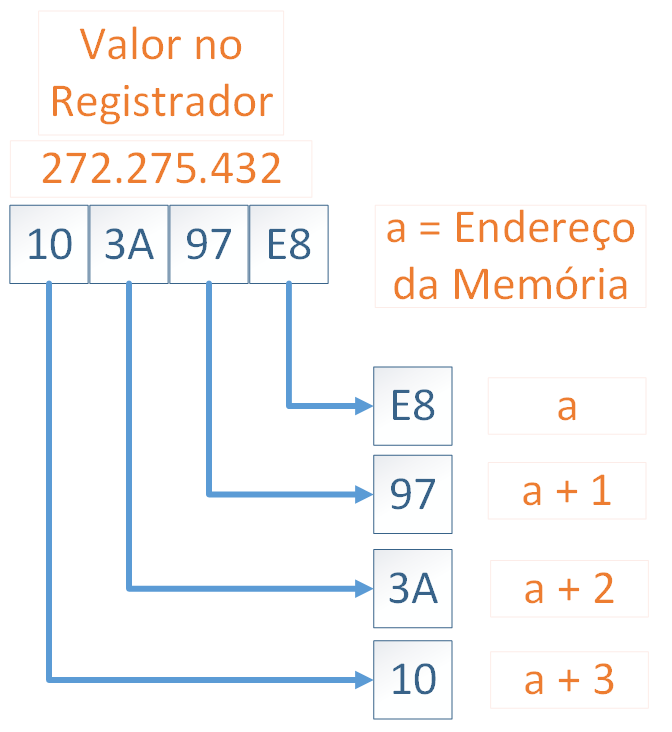
As imagens abaixo representam dois números inteiros armazenados na memória de um microcontrolador qualquer que seja do tipo **Little Endian**. A primeira representa um número de 16 bits, ou seja, uma Word. O segundo, um número de 32 bits, Double Word (DWord).
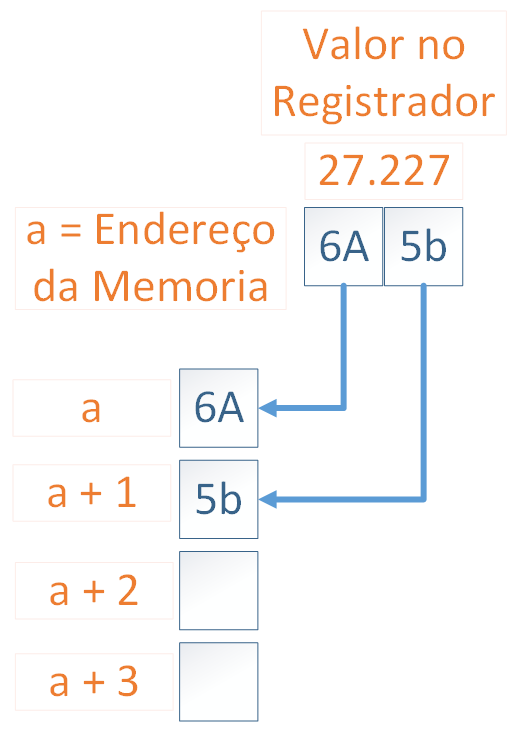
Como pode ver, o byte mais significativo é armazenado no endereço mais baixo da memória, sendo acessado primeiramente, enquanto o byte menos significativo é armazenado posteriormente. Na representação, o endereço de memória começa a contar em `a`.
Vejamos agora como o mesmo número é representado em um sistema Little Endian. A seguir, os mesmos números usados na representação anterior, mas agora utilizando o mecanismo Little Endian para armazená-los.
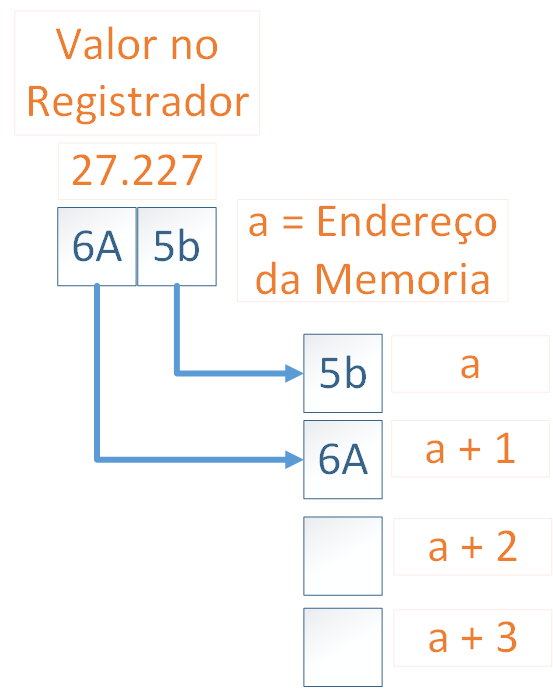
Houve uma época em que, ao transferir dados entre computadores que usavam sistemas diferentes (chamados *byte sex*), como na transmissão de um sistema Little Endian para um sistema Big Endian da string **UNIX**, ocorria o problema conhecido como **NUXI Problem** devido à inversão da string “UNIX”.
Como pode ver, a cada par de bytes, ocorria uma inversão, causando um certo transtorno.
Um exemplo do formato Little Endian em C
Abaixo estão dois códigos que demonstram como um número inteiro é armazenado na memória. O primeiro é um número de 16 bits, um típico inteiro; o segundo, um número de 32 bits, ou seja, um típico inteiro longo.
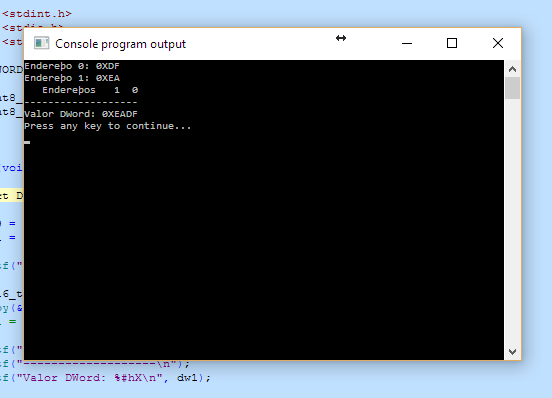
Neste exemplo, mostramos como um inteiro de 2 bytes (16 bits) é armazenado na memória em um formato Little Endian:
#include <stdint.h>
#include <stdio.h>
#include <string.h>
struct DWORD
{
uint8_t a0;
uint8_t a1;
};
int main(void){
struct DWORD dw;
dw.a0 = 0xDF;
dw.a1 = 0xEA;
printf("Endereço 0: %#X\nEndereço 1: %#X\n", dw.a0, dw.a1);
uint32_t dw1;
memcpy(&dw1, &dw, 4);
printf(" Endereços 1 0\n");
printf("-------------------\n");
printf("Valor Word: %#hX\n", dw1);
return 0;
}
——–
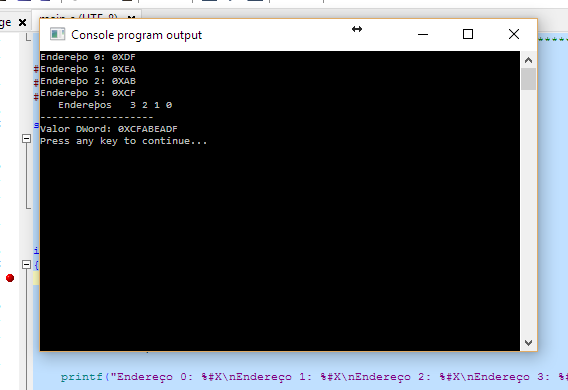
A seguir, um outro exemplo para um inteiro longo de 4 bytes (32 bits), apresentando como é armazenado na memória em um formato Little Endian. Observe as pequenas diferenças no código:
#include <stdint.h>
#include <stdio.h>
#include <string.h>
struct DWORD
{
uint8_t a0;
uint8_t a1;
uint8_t a2;
uint8_t a3;
};
int main(void){
struct DWORD dw;
dw.a0 = 0xDF;
dw.a1 = 0xEA;
dw.a2 = 0xAB;
dw.a3 = 0xCF;
printf("Endereço 0: %#X\nEndereço 1: %#X\nEndereço 2: %#X\nEndereço 3: %#X\n", dw.a0, dw.a1, dw.a2, dw.a3);
uint32_t dw1;
memcpy(&dw1, &dw, 4);
printf(" Endereços 3 2 1 0\n");
printf("-------------------\n");
printf("Valor DWord: %#lX\n", dw1);
return 0;
}
Outras formas de representação
Existem outras formas de representação Endianness, que misturam convenientemente os dois formatos acima. No entanto, não entraremos em detalhes sobre como são apresentadas e utilizadas.
Fontes
- https://en.wikipedia.org/wiki/Endianness
- https://en.wikipedia.org/wiki/Bit_numbering
- https://support.microsoft.com/pt-br/kb/102025
- http://infocenter.arm.com/help/topic/com.arm.doc.dui0552a/I1835.html
- http://david.carybros.com/html/endian_faq.html
- https://www.ietf.org/rfc/ien/ien137.txt
Sobre o Autor
